Simplify the following: (2^(n+5) - 3 * 2^(n-2))/(5 * 2^(n+3))
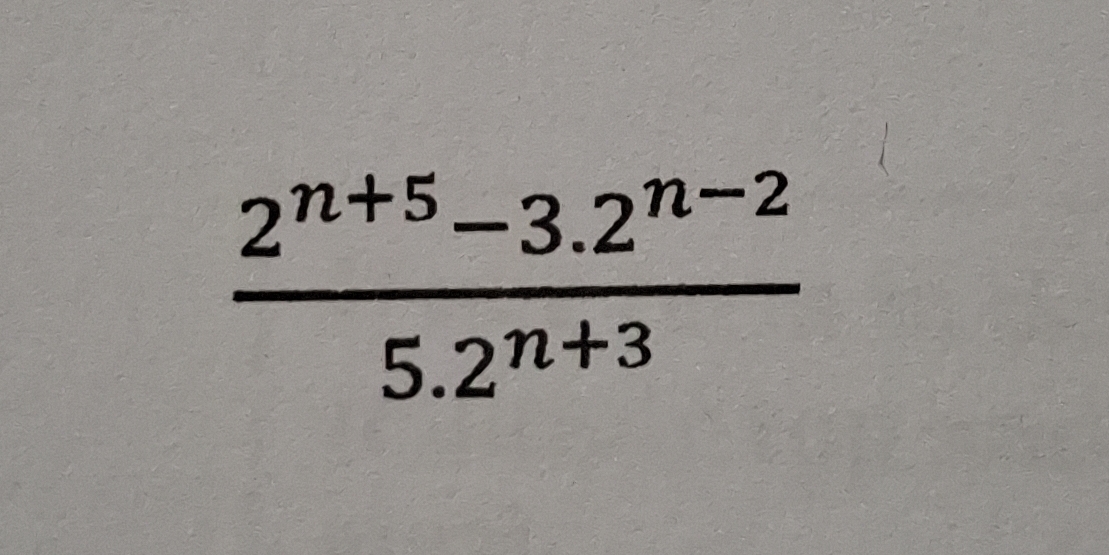
Understand the Problem
The question is asking us to simplify an expression with exponents. We need to use properties of exponents to simplify both the numerator and the denominator, and then see if we can reduce the expression further.
Answer
$\frac{25}{32}$
Answer for screen readers
$\frac{25}{32}$
Steps to Solve
- Rewrite the numerator using exponent rules
We will rewrite $2^{n+5}$ as $2^n \cdot 2^5$ and $2^{n-2}$ as $2^n \cdot 2^{-2}$. This allows us to factor out $2^n$ from the numerator. $$ \frac{2^{n+5} - 3 \cdot 2^{n-2}}{5 \cdot 2^{n+3}} = \frac{2^n \cdot 2^5 - 3 \cdot 2^n \cdot 2^{-2}}{5 \cdot 2^{n+3}} $$
- Factor out $2^n$ from the numerator
We can now factor $2^n$ from the numerator: $$ \frac{2^n (2^5 - 3 \cdot 2^{-2})}{5 \cdot 2^{n+3}} $$
- Simplify the terms within the parenthesis
Let's simplify $2^5$ and $2^{-2}$. $2^5 = 32$ and $2^{-2} = \frac{1}{2^2} = \frac{1}{4}$. Substitute these back into the expression: $$ \frac{2^n (32 - 3 \cdot \frac{1}{4})}{5 \cdot 2^{n+3}} = \frac{2^n (32 - \frac{3}{4})}{5 \cdot 2^{n+3}} $$ Now, simplify the expression inside the parenthesis: $32 - \frac{3}{4} = \frac{32 \cdot 4 - 3}{4} = \frac{128 - 3}{4} = \frac{125}{4}$ So the expression becomes: $$ \frac{2^n \cdot \frac{125}{4}}{5 \cdot 2^{n+3}} $$
-
Rewrite the denominator using exponent rules Now we handle the denominator $5 \cdot 2^{n+3} = 5 \cdot 2^n \cdot 2^3 = 5 \cdot 2^n \cdot 8 = 40 \cdot 2^n$. The whole expression now looks like this: $$ \frac{2^n \cdot \frac{125}{4}}{40 \cdot 2^n} $$
-
Cancel out common terms
Cancel out $2^n$ from the numerator and the denominator: $$ \frac{\frac{125}{4}}{40} $$
- Simplify the fraction
To simplify the fraction, we divide $\frac{125}{4}$ by $40$: $$ \frac{125}{4} \div 40 = \frac{125}{4} \cdot \frac{1}{40} = \frac{125}{4 \cdot 40} = \frac{125}{160} $$ Now, simplify the fraction by dividing both numerator and denominator by their greatest common divisor, which is 5: $$ \frac{125 \div 5}{160 \div 5} = \frac{25}{32} $$
$\frac{25}{32}$
More Information
The final simplified answer is $\frac{25}{32}$. This result is obtained by applying exponent rules, factoring, and simplifying the resulting fraction.
Tips
A common mistake is incorrectly applying the exponent rules, especially when dealing with negative exponents or when factoring. Also, arithmetic errors when simplifying fractions are common. So, it's important to double-check the arithmetic operations and exponent rules application.
AI-generated content may contain errors. Please verify critical information