Evaluate the limit: lim (x->4) (x^2 - 16) / (x^2 - 5x + 6)
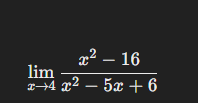
Understand the Problem
The question requires us to evaluate the limit of a rational function as x approaches 4. This involves techniques such as factoring and simplifying to resolve any indeterminate forms.
Answer
0
Answer for screen readers
0
Steps to Solve
- Factor the numerator and denominator
Factor $x^2 - 16$ as a difference of squares, and factor the quadratic in the denominator. $$ x^2 - 16 = (x - 4)(x + 4) $$ $$ x^2 - 5x + 6 = (x - 2)(x - 3) $$
- Rewrite the limit expression
Substitute the factored forms into the limit expression:
$$ \lim_{x \to 4} \frac{(x - 4)(x + 4)}{(x - 2)(x - 3)} $$
- Check for direct substitution
If we directly substitute $x = 4$ into the expression we obtain: $$ \frac{(4 - 4)(4 + 4)}{(4 - 2)(4 - 3)} = \frac{0 \cdot 8}{2 \cdot 1} = \frac{0}{2} = 0 $$
- State the final answer
Since direct substitution does not result in an indeterminate form, the limit is 0.
0
More Information
The function converges to 0 as x approaches 4.
Tips
A common mistake is to incorrectly factor the quadratic expressions. Another mistake is to assume that since the numerator contains $(x-4)$, the limit automatically does not exist or is indeterminate. However, here the denominator does not have this factor, and direct substitution gives us the limit.
AI-generated content may contain errors. Please verify critical information