Evaluate the limit: lim (x->1) (x^(1/6) - 1) / (x - 1)
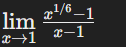
Understand the Problem
The question asks to evaluate the limit of the function (x^(1/6) - 1) / (x - 1) as x approaches 1. We'll need to use calculus techniques, such as L'Hopital's rule, or algebraic manipulation to find the limit.
Answer
$\frac{1}{6}$
Answer for screen readers
$\frac{1}{6}$
Steps to Solve
-
Recognize the indeterminate form
When we substitute $x = 1$ into the expression, we get $\frac{1^{1/6} - 1}{1 - 1} = \frac{0}{0}$, which is an indeterminate form. This means we can apply L'Hopital's Rule.
-
Apply L'Hopital's Rule
L'Hopital's Rule states that if $\lim_{x\to c} \frac{f(x)}{g(x)}$ is of the form $\frac{0}{0}$ or $\frac{\infty}{\infty}$, then $\lim_{x\to c} \frac{f(x)}{g(x)} = \lim_{x\to c} \frac{f'(x)}{g'(x)}$, provided the limit exists.
In our case, $f(x) = x^{1/6} - 1$ and $g(x) = x - 1$. We need to find their derivatives.
-
Calculate the derivatives
The derivative of $f(x)$ with respect to $x$ is: $f'(x) = \frac{d}{dx}(x^{1/6} - 1) = \frac{1}{6}x^{\frac{1}{6} - 1} = \frac{1}{6}x^{-5/6}$
The derivative of $g(x)$ with respect to $x$ is: $g'(x) = \frac{d}{dx}(x - 1) = 1$
-
Evaluate the limit of the derivatives
Now we evaluate the limit of the ratio of the derivatives: $\lim_{x\to 1} \frac{f'(x)}{g'(x)} = \lim_{x\to 1} \frac{\frac{1}{6}x^{-5/6}}{1} = \lim_{x\to 1} \frac{1}{6}x^{-5/6}$
Substitute $x = 1$ into the expression: $\frac{1}{6}(1)^{-5/6} = \frac{1}{6}(1) = \frac{1}{6}$
$\frac{1}{6}$
More Information
L'Hopital's Rule is a powerful tool for evaluating limits of indeterminate forms ($0/0$ or $\infty/\infty$). Applying it correctly involves taking the derivative of the numerator and the denominator separately, then evaluating the limit of the resulting expression.
Tips
A common mistake is to try to apply L'Hopital's Rule when the limit is not in an indeterminate form. Another mistake is taking the derivative of the entire fraction instead of the numerator and denominator separately.
AI-generated content may contain errors. Please verify critical information