Evaluate the integral ∫ (x^2 + 4) / x^2 dx

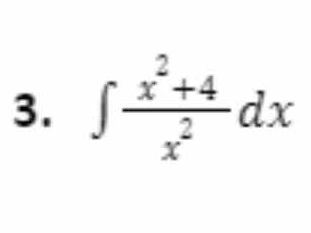
Understand the Problem

The question is asking us to evaluate the integral of the function (x^2 + 4) / x^2 with respect to x. This involves simplifying the expression and determining its antiderivative.

Answer

$$ x - \frac{4}{x} + C $$

Steps to Solve

Simplifying the Integral

First, we can simplify the integrand $\frac{x^2 + 4}{x^2}$ by breaking it into two separate fractions: $$ \frac{x^2 + 4}{x^2} = \frac{x^2}{x^2} + \frac{4}{x^2} = 1 + \frac{4}{x^2} $$

Setting Up the Integral

Now, we can rewrite the integral: $$ \int \left(1 + \frac{4}{x^2}\right) dx $$

Integrating Each Term

We can now integrate each term separately:

The integral of $1$ with respect to $x$ is $x$.
The integral of $\frac{4}{x^2}$ can be rewritten as $4x^{-2}$. The integral of $x^{-2}$ is $-\frac{1}{x}$.

So we get: $$ \int \left(1 + \frac{4}{x^2}\right) dx = x - \frac{4}{x} + C $$ where $C$ is the constant of integration.

The final result of the integral is: $$ x - \frac{4}{x} + C $$

More Information

This integral can be useful in various applications, including physics and engineering, where you need to evaluate functions that model rates of change and areas under curves. The constant of integration $C$ represents any constant since there are infinitely many antiderivatives for a given function.

Tips

Not simplifying: Some students may forget to simplify the integrand before integrating, which can lead to more complicated calculations.
Misapplying integral rules: It is important to correctly apply integration rules for each separated term.
Forgetting the constant of integration: Always remember to add the constant $C$ at the end of your integration.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!