Evaluate the integral of sin(5x)dx.
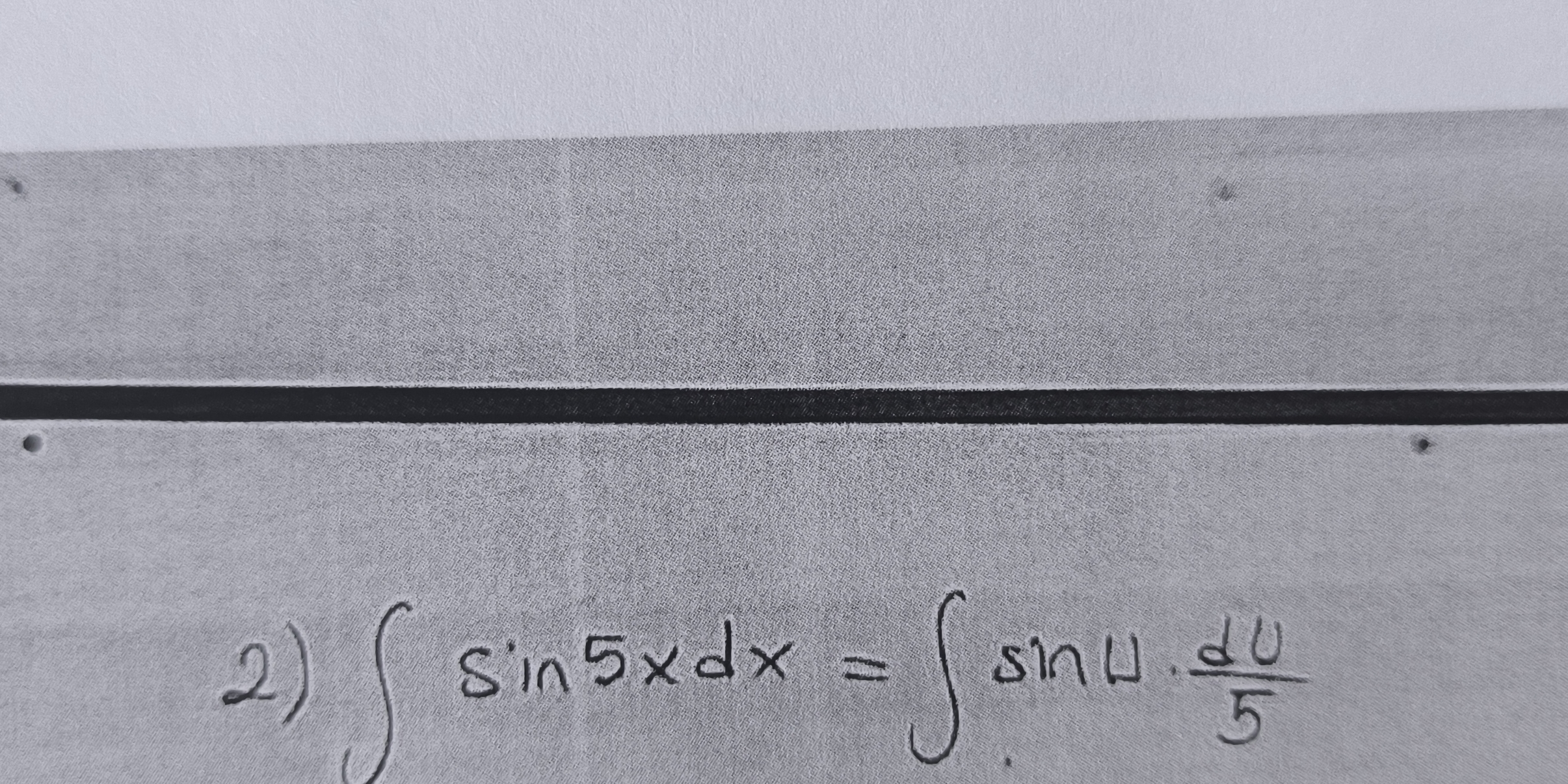
Understand the Problem
The question asks to evaluate the integral of sin(5x)dx. This involves using u-substitution, where u = 5x, and finding the antiderivative of sine, which is -cosine.
Answer
$-\frac{1}{5} \cos(5x) + C$
Answer for screen readers
$-\frac{1}{5} \cos(5x) + C$
Steps to Solve
-
Perform u-substitution Let $u = 5x$. Then, $\frac{du}{dx} = 5$. So, $dx = \frac{du}{5}$.
-
Rewrite the integral in terms of u Substitute $u$ and $du$ into the original integral: $$ \int \sin(5x) , dx = \int \sin(u) , \frac{du}{5} $$
-
Pull out the constant $$ \int \sin(u) , \frac{du}{5} = \frac{1}{5} \int \sin(u) , du $$
-
Integrate sin(u) The integral of $\sin(u)$ is $-\cos(u)$. $$ \frac{1}{5} \int \sin(u) , du = \frac{1}{5} (-\cos(u)) + C $$
-
Substitute back for x Replace $u$ with $5x$: $$ \frac{1}{5} (-\cos(u)) + C = -\frac{1}{5} \cos(5x) + C $$
$-\frac{1}{5} \cos(5x) + C$
More Information
The indefinite integral represents a family of functions whose derivative is $sin(5x)$. The "+ C" represents the constant of integration, an arbitrary constant.
Tips
A common mistake is forgetting the constant of integration, C. Another common mistake is not correctly performing the u-substitution and forgetting to solve for $dx$ in terms of $du$. Also, the derivative of $\cos(x)$ is $-\sin(x)$, thus the integral of $\sin(x)$ is $-\cos(x)$. Forgetting the negative sign is a common mistake.
AI-generated content may contain errors. Please verify critical information