Evaluate the integral of e^(2*log(x)) dx
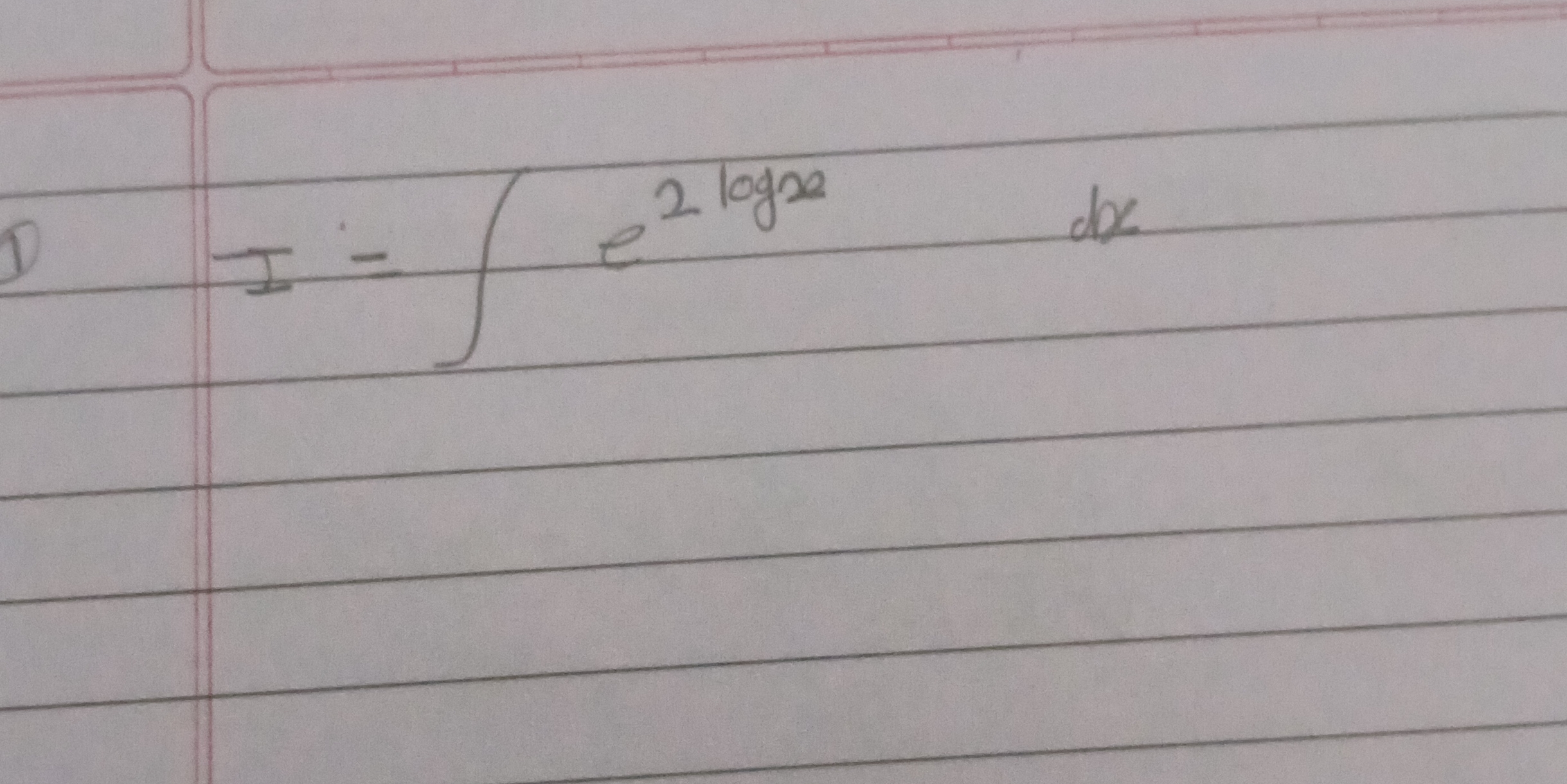
Understand the Problem
The question asks to evaluate the integral of e^(2*log(x)) with respect to x. This involves simplifying the integrand using properties of logarithms and exponentials before performing the integration.
Answer
$\frac{x^3}{3} + C$
Answer for screen readers
$I = \frac{x^3}{3} + C$
Steps to Solve
- Simplify the exponent using logarithm properties
We can use the power rule of logarithms, which states that $a \log(x) = \log(x^a)$. Applying this rule, we can rewrite the exponent:
$2 \log(x) = \log(x^2)$
- Substitute back into the integral
Now substitute this back into the original integral:
$I = \int e^{\log(x^2)} dx$
- Simplify the integrand using the inverse relationship between exponentials and logarithms
Since $e^{\log(u)} = u$, we can further simplify the integrand:
$e^{\log(x^2)} = x^2$
Thus, the integral becomes:
$I = \int x^2 dx$
- Evaluate the simplified integral
Now, integrate $x^2$ with respect to $x$:
$I = \int x^2 dx = \frac{x^3}{3} + C$ where $C$ is the constant of integration.
$I = \frac{x^3}{3} + C$
More Information
The integral of $e^{2 \log{x}}$ simplifies to $\frac{x^3}{3} + C$ by using properties of logarithms and exponentials to simplify the integrand before integrating. Remember to include the constant of integration $C$.
Tips
A common mistake is forgetting the constant of integration, $C$. Another mistake could be misapplying the logarithm or exponential rules during the simplification process.
AI-generated content may contain errors. Please verify critical information