Evaluate the following limit: $\lim_{x \to 0} \frac{\sqrt{x+1} - \sqrt{2x+1}}{\sqrt{3x+4} - \sqrt{2x+4}}$
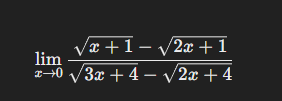
Understand the Problem
The question is asking to calculate the limit of a function as x approaches 0. The function involves square roots in both the numerator and the denominator. This will likely require algebraic manipulation, such as rationalizing the numerator and/or denominator, to evaluate the limit.
Answer
$-2$
Answer for screen readers
$-2$
Steps to Solve
- Rationalize the numerator Multiply the numerator and denominator by the conjugate of the numerator: $\sqrt{x+1} + \sqrt{2x+1}$.
$$ \lim_{x \to 0} \frac{\sqrt{x+1}-\sqrt{2x + 1}}{\sqrt{3x+4}-\sqrt{2x+4}} \cdot \frac{\sqrt{x+1}+\sqrt{2x + 1}}{\sqrt{x+1}+\sqrt{2x + 1}} $$
$$ = \lim_{x \to 0} \frac{(x+1) - (2x+1)}{(\sqrt{3x+4}-\sqrt{2x+4})(\sqrt{x+1}+\sqrt{2x + 1})} $$
$$ = \lim_{x \to 0} \frac{-x}{(\sqrt{3x+4}-\sqrt{2x+4})(\sqrt{x+1}+\sqrt{2x + 1})} $$
- Rationalize the denominator Multiply the numerator and denominator by the conjugate of $\sqrt{3x+4} - \sqrt{2x+4}$, which is $\sqrt{3x+4} + \sqrt{2x+4}$.
$$ \lim_{x \to 0} \frac{-x}{(\sqrt{3x+4}-\sqrt{2x+4})(\sqrt{x+1}+\sqrt{2x + 1})} \cdot \frac{\sqrt{3x+4}+\sqrt{2x+4}}{\sqrt{3x+4}+\sqrt{2x+4}} $$
$$ = \lim_{x \to 0} \frac{-x(\sqrt{3x+4}+\sqrt{2x+4})}{((3x+4)-(2x+4))(\sqrt{x+1}+\sqrt{2x + 1})} $$
$$ = \lim_{x \to 0} \frac{-x(\sqrt{3x+4}+\sqrt{2x+4})}{x(\sqrt{x+1}+\sqrt{2x + 1})} $$
- Simplify the expression Cancel out the $x$ term in the numerator and the denominator.
$$ \lim_{x \to 0} \frac{-(\sqrt{3x+4}+\sqrt{2x+4})}{\sqrt{x+1}+\sqrt{2x + 1}} $$
- Evaluate the limit Substitute $x=0$ into the simplified expression.
$$ \frac{-(\sqrt{3(0)+4}+\sqrt{2(0)+4})}{\sqrt{(0)+1}+\sqrt{2(0) + 1}} = \frac{-(\sqrt{4}+\sqrt{4})}{\sqrt{1}+\sqrt{1}} $$
$$ = \frac{-(2+2)}{1+1} = \frac{-4}{2} = -2 $$
$-2$
More Information
The limit of the given function as $x$ approaches $0$ is $-2$.
Tips
A common mistake is not properly rationalizing the numerator or denominator, which can lead to an indeterminate form and prevent simplification. Another mistake is incorrectly applying the conjugate or making algebraic errors during the simplification process.
AI-generated content may contain errors. Please verify critical information