Evaluate the following expression using the order of operations: (2+3) * 4 + 3^3 - (1*5) =
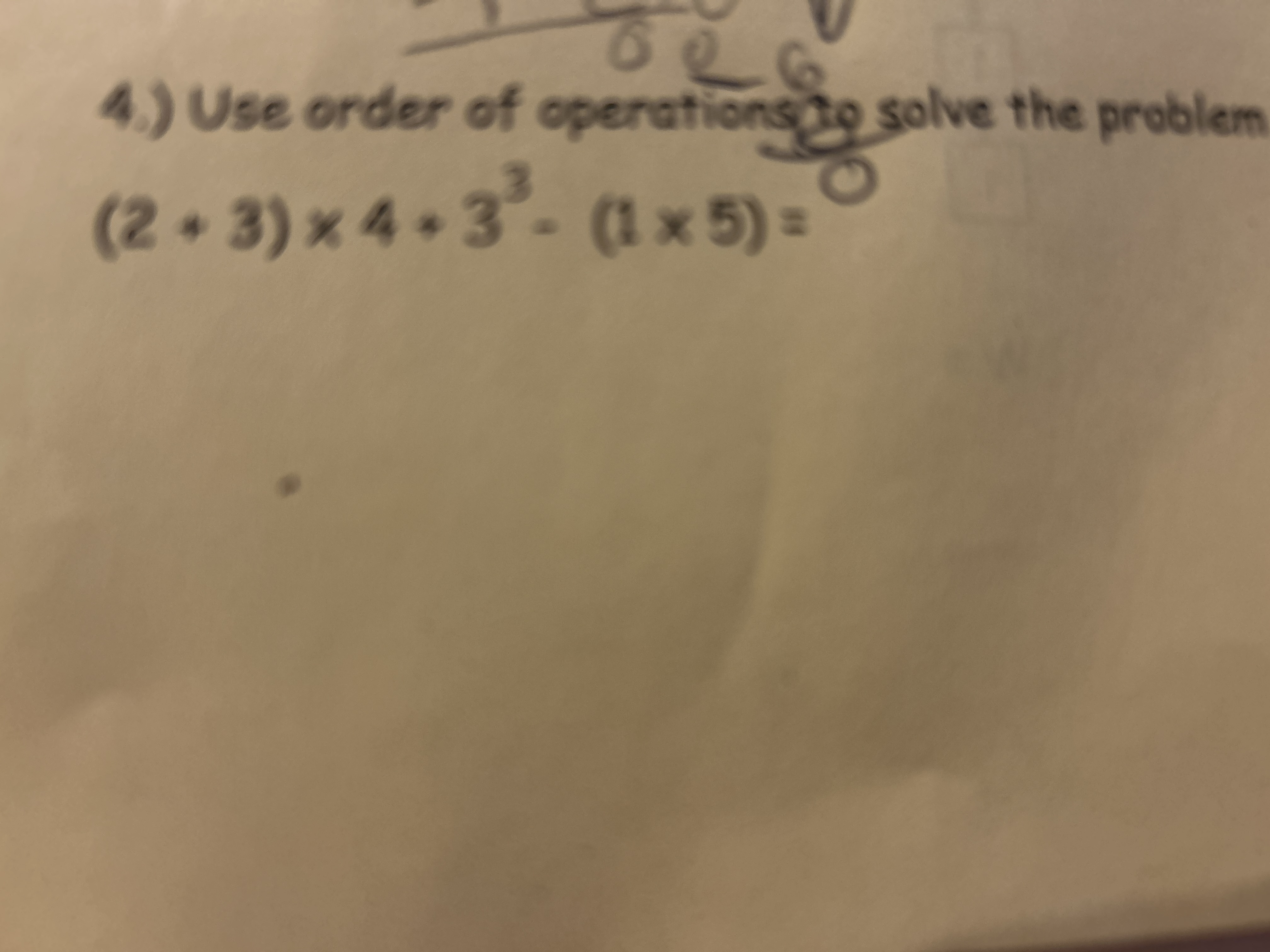
Understand the Problem
The question asks us to evaluate the arithmetic expression (2+3)x4+3^3 - (1x5) using the order of operations (PEMDAS/BODMAS). This means we need to perform the operations within the parentheses first, followed by exponents, then multiplication and division (from left to right), and finally addition and subtraction (from left to right).
Answer
42
Answer for screen readers
$42$
Steps to Solve
-
Evaluate the first parenthesis Add 2 and 3: $2 + 3 = 5$
-
Evaluate the second parenthesis Multiply 1 and 5: $1 \times 5 = 5$
-
Evaluate the exponent Calculate 3 cubed: $3^3 = 3 \times 3 \times 3 = 27$
-
Perform the multiplication Multiply 5 and 4: $5 \times 4 = 20$
-
Rewrite the expression Substitute the results back into the expression: $20 + 27 - 5$
-
Perform the addition Add 20 and 27: $20 + 27 = 47$
-
Perform the subtraction Subtract 5 from 47: $47 - 5 = 42$
$42$
More Information
The order of operations (PEMDAS/BODMAS) is crucial for solving mathematical expressions correctly. It dictates the sequence in which calculations are performed: Parentheses/Brackets, Exponents/Orders, Multiplication and Division (from left to right), Addition and Subtraction (from left to right).
Tips
A common mistake is not following the correct order of operations. For example, performing the addition before the multiplication or exponentiation would lead to an incorrect answer. Another mistake is mishandling the exponent.
AI-generated content may contain errors. Please verify critical information