Evaluate the definite integral: π ∫ [ (x³ + 3)² - (4)² ] dx from 1 to 2.
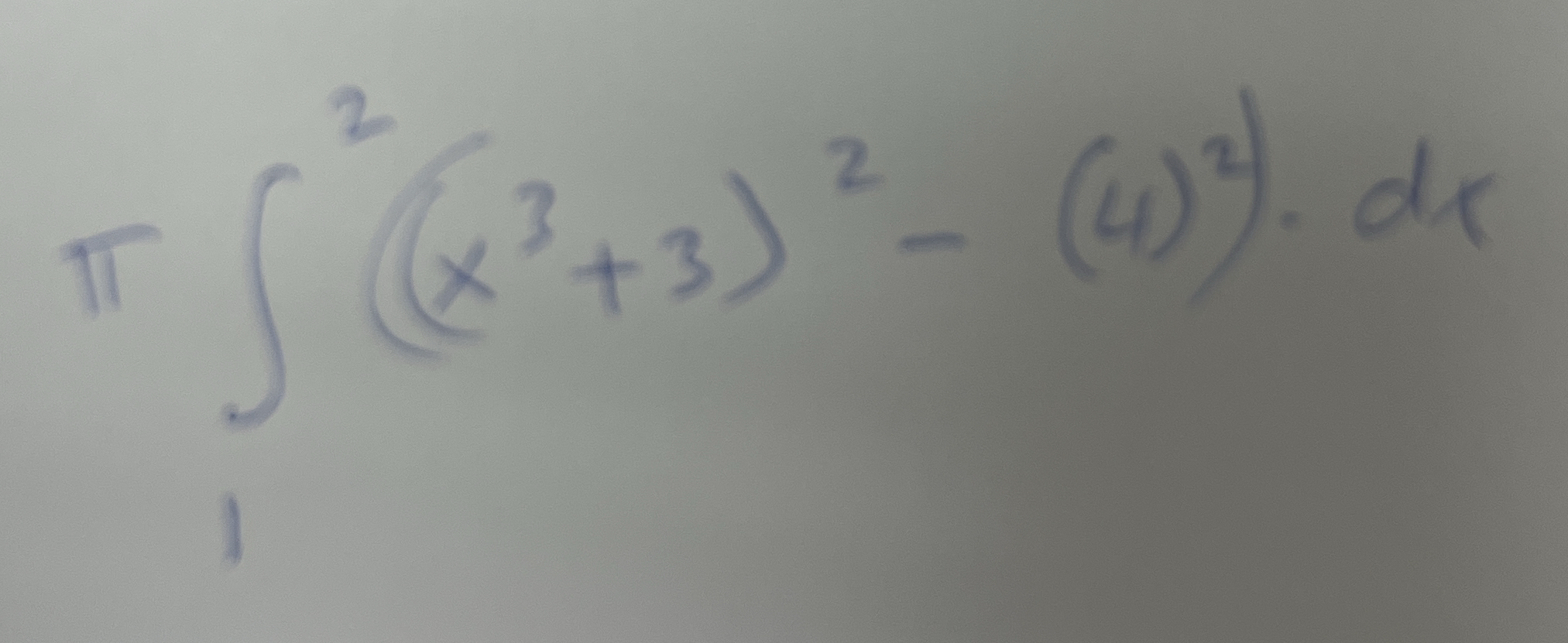
Understand the Problem
The question asks us to evaluate a definite integral involving polynomial functions. We need to find the antiderivative of the integrand and evaluate it at the limits of integration, which are 1 and 2.
Answer
$\frac{471\pi}{14}$
Answer for screen readers
$\frac{471\pi}{14}$
Steps to Solve
-
Expand the terms inside the integral Expand $(x^3+3)^2$ and $4^2$. $$ (x^3+3)^2 = x^6 + 6x^3 + 9 $$ $$ 4^2 = 16 $$ So the integrand becomes $$ (x^6 + 6x^3 + 9) - 16 = x^6 + 6x^3 - 7 $$
-
Rewrite the integral Now, rewrite the integral with the simplified integrand: $$ \pi \int_{1}^{2} (x^6 + 6x^3 - 7) dx $$
-
Find the antiderivative Find the antiderivative of $x^6 + 6x^3 - 7$ with respect to $x$: $$ \int (x^6 + 6x^3 - 7) dx = \frac{x^7}{7} + \frac{6x^4}{4} - 7x + C = \frac{x^7}{7} + \frac{3x^4}{2} - 7x + C $$
-
Evaluate the definite integral Evaluate the antiderivative at the upper and lower limits of integration (2 and 1, respectively) and subtract: $$ \left[ \frac{x^7}{7} + \frac{3x^4}{2} - 7x \right]_{1}^{2} = \left( \frac{2^7}{7} + \frac{3(2^4)}{2} - 7(2) \right) - \left( \frac{1^7}{7} + \frac{3(1^4)}{2} - 7(1) \right) $$ $$ = \left( \frac{128}{7} + \frac{3(16)}{2} - 14 \right) - \left( \frac{1}{7} + \frac{3}{2} - 7 \right) $$ $$ = \frac{128}{7} + 24 - 14 - \frac{1}{7} - \frac{3}{2} + 7 $$ $$ = \frac{127}{7} + 17 - \frac{3}{2} = \frac{254}{14} + \frac{238}{14} - \frac{21}{14} = \frac{471}{14} $$
-
Multiply by $\pi$ Multiply the result by $\pi$: $$ \pi \left( \frac{471}{14} \right) = \frac{471\pi}{14} $$
$\frac{471\pi}{14}$
More Information
The definite integral evaluates to $\frac{471\pi}{14}$. This is the exact value of the integral.
Tips
A common mistake is to forget to distribute $\pi$ after evaluating the integral or making an error when simplifying fractions. Another common mistake is incorrectly calculating the antiderivative.
AI-generated content may contain errors. Please verify critical information