Evaluate: $\frac{5}{7} + \frac{5}{9} + \frac{5}{3}$
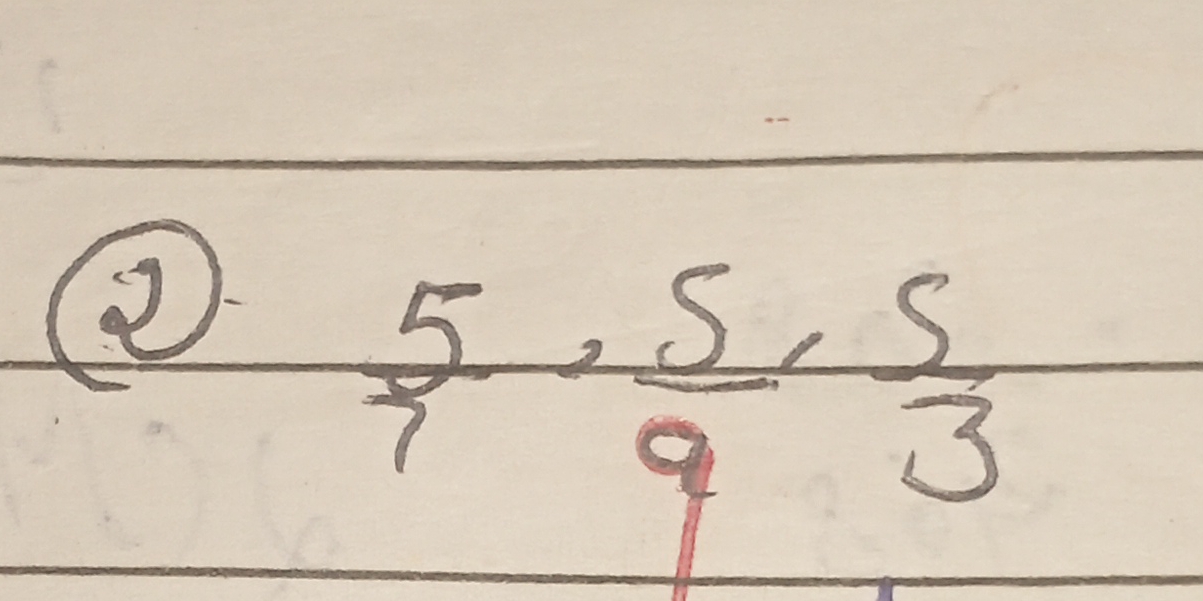
Understand the Problem
The question is asking to perform the following calculation: $\frac{5}{7} + \frac{5}{9} + \frac{5}{3}$. We need to find a common denominator and sum the fractions.
Answer
$\frac{185}{63}$
Answer for screen readers
$\frac{185}{63}$ or $2\frac{59}{63}$
Steps to Solve
-
Find the Least Common Denominator (LCD) To add these fractions, we need to find the least common denominator (LCD) of 7, 9, and 3. The prime factorization of each number is:
- 7 = 7
- 9 = 3 x 3 = $3^2$
- 3 = 3 The LCD is the product of the highest powers of all prime factors present in the denominators. Therefore, LCD = 7 x $3^2$ = 7 x 9 = 63.
-
Convert each fraction to an equivalent fraction with the LCD We need to convert each fraction to have a denominator of 63.
- $\frac{5}{7} = \frac{5 \times 9}{7 \times 9} = \frac{45}{63}$
- $\frac{5}{9} = \frac{5 \times 7}{9 \times 7} = \frac{35}{63}$
- $\frac{5}{3} = \frac{5 \times 21}{3 \times 21} = \frac{105}{63}$
-
Add the fractions Now that all fractions have the same denominator, we can add them: $\frac{45}{63} + \frac{35}{63} + \frac{105}{63} = \frac{45 + 35 + 105}{63} = \frac{185}{63}$
-
Simplify the fraction (if possible) The fraction $\frac{185}{63}$ is already in its simplest form, since 185 and 63 do not have any common factors other than 1. We can leave the answer as an improper fraction, or convert it to a mixed number. To convert the improper fraction to a mixed number: $185 \div 63 = 2$ with a remainder of $59$. So, the mixed number is $2\frac{59}{63}$.
$\frac{185}{63}$ or $2\frac{59}{63}$
More Information
The fraction $\frac{185}{63}$ is an improper fraction. When converted to a mixed number, it equals $2\frac{59}{63}$.
Tips
A common mistake is incorrectly calculating the Least Common Denominator (LCD). Another mistake is not multiplying both the numerator and denominator by the same number when converting to equivalent fractions. Finally, arithmetic errors when adding the numerators is also a possible mistake.
AI-generated content may contain errors. Please verify critical information