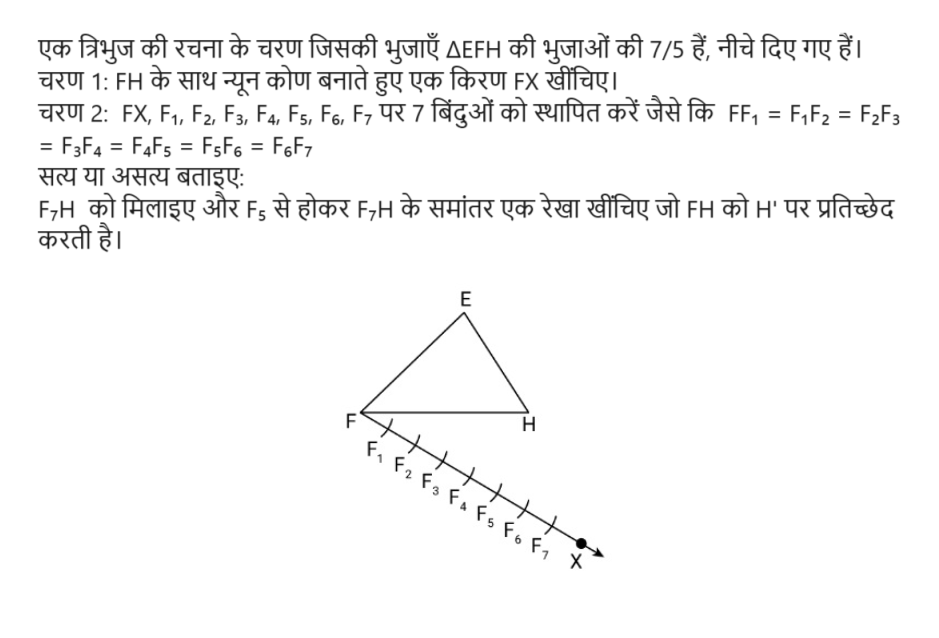
एक त्रिभुज की रचना के चरण जिसकी भुजाएँ △EFH की भुजाओं की 7/5 हैं, नीचे दिए गए हैं। चरण 1: FH के साथ न्यून कोण बनाते हुए एक किरण FX खींचिए। चरण 2: FX, F1, F2, F3, F4, F5, F6, F7 पर... एक त्रिभुज की रचना के चरण जिसकी भुजाएँ △EFH की भुजाओं की 7/5 हैं, नीचे दिए गए हैं। चरण 1: FH के साथ न्यून कोण बनाते हुए एक किरण FX खींचिए। चरण 2: FX, F1, F2, F3, F4, F5, F6, F7 पर 7 बिंदुओं को स्थापित करें जैसे कि FF₁ = F₁F2 = F2F3 = F3F4 = F4F5 = F5F6 = F6F7 सत्य या असत्य बताइए: F7H को मिलाइए और F5 से होकर F7H के समांतर एक रेखा खींचिए जो FH को H' पर प्रतिच्छेद करती है। Read more

Steps to Solve

1. समानुपात को समझना हमें एक त्रिभुज बनाना है जिसकी भुजाएँ दिए गए त्रिभुज की भुजाओं की $7/5$ गुना हों। इसका अर्थ है कि हम त्रिभुज की भुजाओं को $7/5$ के कारक से बढ़ा रहे हैं।

2. किरण FX पर बिंदु स्थापित करना किरण FX पर 7 बिंदु इस प्रकार स्थापित करना कि $FF_1 = F_1F_2 = F_2F_3 = F_3F_4 = F_4F_5 = F_5F_6 = F_6F_7$, एक आधार रेखा बनाने का एक तरीका है जिसका उपयोग हम समानुपातिक भुजाओं वाला एक त्रिभुज बनाने के लिए करेंगे। चूँकि हम $7/5$ के कारक से बढ़ा रहे हैं, इसलिए 7 बराबर खंडों में विभाजित करना समझ में आता है ताकि हम बढ़े हुए त्रिभुज के लिए एक उपयुक्त बिंदु पा सकें।

3. $F_7H$ से मिलाना और समानांतर रेखा खींचना $F_7H$ को मिलाइए। अब, $F_5$ से होकर $F_7H$ के समानांतर एक पंक्ति खींचिए। यह रेखा $FH$ को एक बिंदु $H'$ पर काटेगी। समान त्रिभुजों के गुणों के अनुसार, $FH'$ की लंबाई $FH$ का $5/7$ होगी। परंतु हमें 7/5 गुना करना है, इसलिए हमें $F_5$ से नहीं, बल्कि $F_7H$ के समानांतर $F_7$ से होकर एक रेखा खींचनी चाहिए।

4. निष्कर्ष इसलिए, यह कथन गलत है क्योंकि नए त्रिभुज की भुजाओ की लम्बाई मूल त्रिभुज की भुजाओं की 5/7 होगी, न की 7/5.