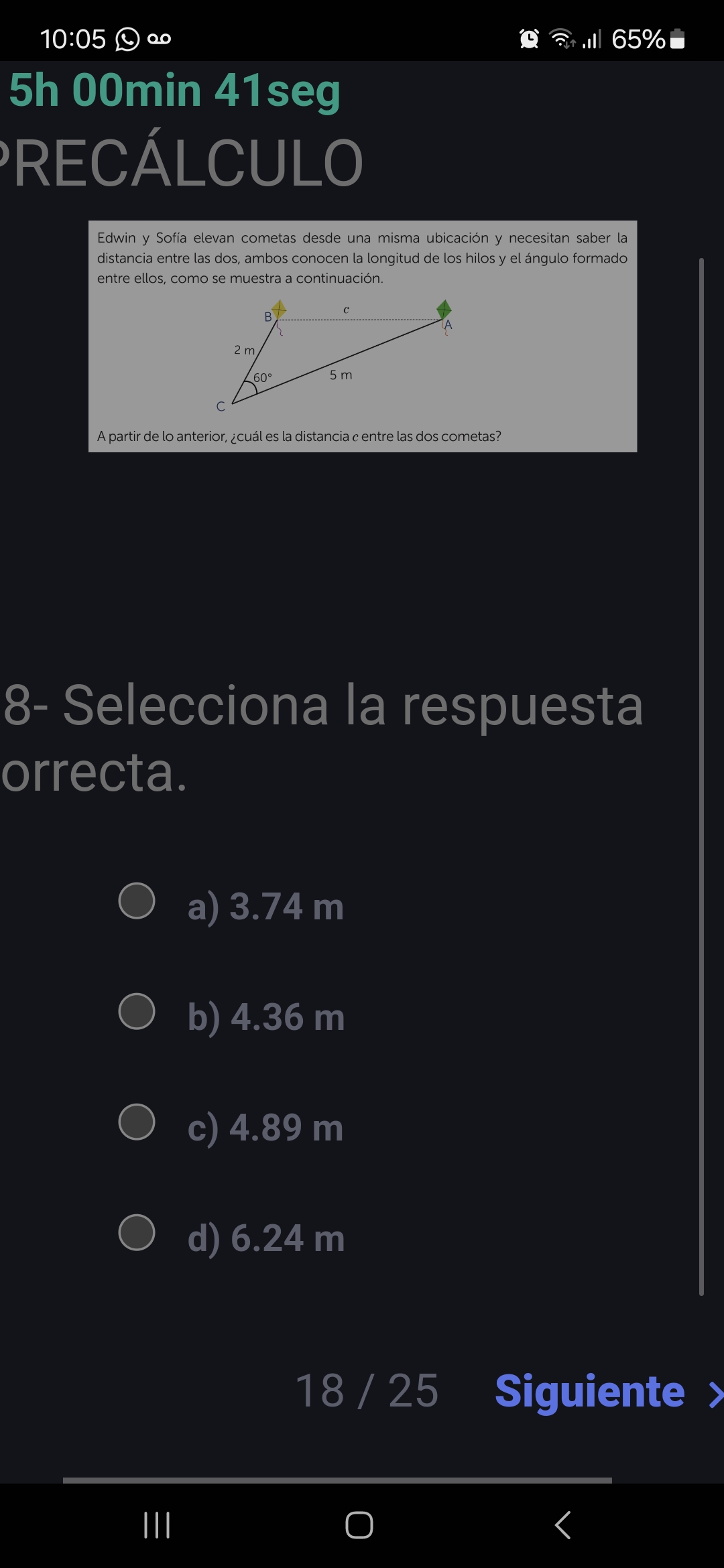
Edwin y Sofía elevan cometas desde una misma ubicación y necesitan saber la distancia entre las dos, ambos conocen la longitud de los hilos y el ángulo formado entre ellos, como se... Edwin y Sofía elevan cometas desde una misma ubicación y necesitan saber la distancia entre las dos, ambos conocen la longitud de los hilos y el ángulo formado entre ellos, como se muestra a continuación. A partir de lo anterior, ¿cuál es la distancia c entre las dos cometas?
Understand the Problem
El problema plantea una situación donde Edwin y Sofía están volando cometas desde la misma ubicación. Se conoce la longitud de los hilos de cada cometa (2m y 5m) y el ángulo entre ellos (60 grados). El objetivo es determinar la distancia entre las dos cometas. Podemos usar la ley de los cosenos para resolver este problema.
Answer
$c \approx 4.36 \text{ m}$
Answer for screen readers
$c \approx 4.36 \text{ m}$
Steps to Solve
- Identify the knowns
We know the lengths of two sides of the triangle and the angle between them. Let $a = 5$ m and $b = 2$ m, and the angle $C = 60^\circ$. We want to find the length of the side $c$.
- Apply the Law of Cosines
The Law of Cosines states: $c^2 = a^2 + b^2 - 2ab \cos(C)$
- Substitute the known values
Substitute the known values into the Law of Cosines equation: $c^2 = 5^2 + 2^2 - 2(5)(2) \cos(60^\circ)$
- Calculate $\cos(60^\circ)$
$\cos(60^\circ) = \frac{1}{2}$
- Plug $\cos(60^\circ)$ in and simplify
Plug the cosine value back into the equation and simplify: $c^2 = 25 + 4 - 20(\frac{1}{2})$ $c^2 = 29 - 10$ $c^2 = 19$
- Solve for c
Take the square root of both sides to solve for $c$: $c = \sqrt{19}$
- Approximate the square root
$c \approx 4.36$ m
$c \approx 4.36 \text{ m}$
More Information
The Law of Cosines is a generalization of the Pythagorean theorem, which only applies to right triangles. The Law of Cosines can be used for any triangle
Tips
A common mistake is forgetting to take the square root at the end to find $c$ after calculating $c^2$. Another mistake is using the wrong trigonometric function or incorrectly substituting values into the Law of Cosines formula. Also ensure your calculator is in degree mode when evaluating the cosine function.
AI-generated content may contain errors. Please verify critical information