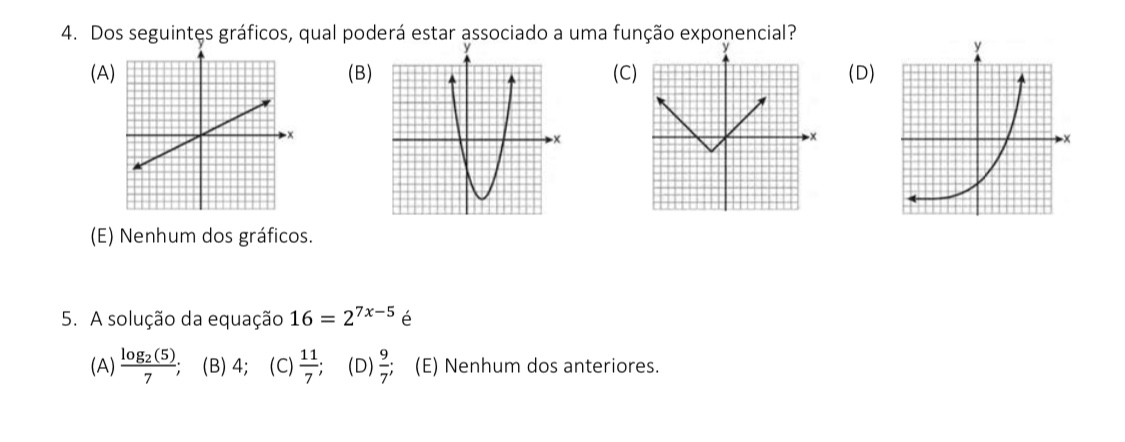
Dos seguintes gráficos, qual poderá estar associado a uma função exponencial? A solução da equação 16 = 27^(7x-5) é?

Steps to Solve

1. Identificação do gráfico da função exponencial

Um gráfico de uma função exponencial tem a forma geral $y = a \cdot b^x$, onde $a > 0$ e $b > 1$. Ele sempre cresce ou decresce rapidamente, dependendo da base $b$.

Analisando os gráficos apresentados, o gráfico que se assemelha a uma função exponencial é o gráfico (D), pois ele mostra um crescimento contínuo e suave, característico das funções exponenciais.

2. Resolvendo a equação exponencial

Dada a equação $16 = 27^{7x - 5}$, primeiro vamos reescrever 16 e 27 em termos de potências de 2 e 3, respectivamente:

$$16 = 2^4 \quad \text{e} \quad 27 = 3^3$$

Assim, podemos transformar a equação:

$$2^4 = (3^3)^{7x - 5}$$

3. Simplificação da equação

Ao simplificar a direita, obtemos:

$$2^4 = 3^{(21x - 15)}$$

Essa forma revela que as duas bases (2 e 3) não são as mesmas. Para resolver, devemos usar logaritmos:

$$4 \log(2) = (21x - 15) \log(3)$$

4. Isolando x

Agora, podemos isolar $x$:

$$21x - 15 = \frac{4 \log(2)}{\log(3)}$$

$$21x = \frac{4 \log(2)}{\log(3)} + 15$$

$$x = \frac{\frac{4 \log(2)}{\log(3)} + 15}{21}$$

5. Simplificação e resposta

Calculando a expressão de $x$ em termos de logaritmos:

$$x = \frac{4 \log(2) + 15 \log(3)}{21 \log(3)}$$

Para uma solução mais específica, o enunciado pede a solução em termos da forma dada nas alternativas, onde precisamos manipular:

$$16 = 2^{4} = 27^{7x-5}$$

Identificando a solução correta, pode-se calcular ou estimar a partir das opções dadas.