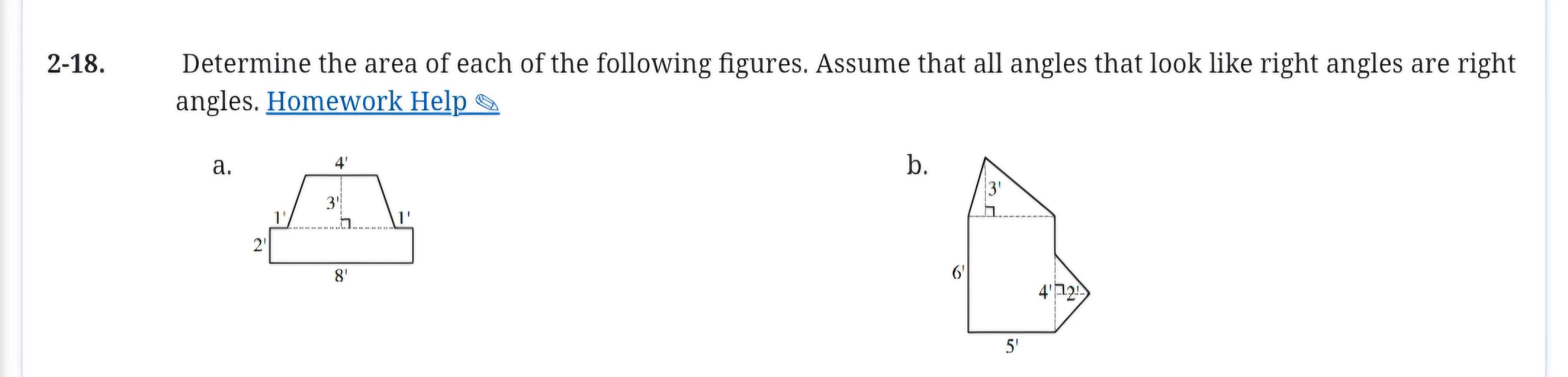
Determine the area of each of the following figures. Assume that all angles that look like right angles are right angles.

Steps to Solve

1. Calculate the area of figure a

To find the area of figure a, we recognize it as a trapezoid, which can be split into a rectangle and two triangles.

• Area of the rectangle: The base is $8'$ and the height is $3' + 1' = 4'$.

  $$ A_{\text{rectangle}} = \text{base} \times \text{height} = 8' \times 4' = 32 , \text{square feet} $$

• Area of the two triangles: The top base is $4'$ and each triangle has a height of $1'$.

  $$ A_{\text{triangle}} = \frac{1}{2} \times \text{base} \times \text{height} $$

  The total area of the two triangles can be calculated as follows:

  $$ A_{\text{triangles}} = 2 \times \left(\frac{1}{2} \times 4' \times 1'\right) = 4 , \text{square feet} $$

2. Add the areas together for figure a

Combine the areas of the rectangle and the triangles:

$$ A_{\text{total_a}} = A_{\text{rectangle}} + A_{\text{triangles}} = 32 , \text{square feet} + 4 , \text{square feet} = 36 , \text{square feet} $$

3. Calculate the area of figure b

To find the area of figure b, we separate it into a rectangle and a triangle.

• Area of the rectangle: The base is $5'$ and the height is $6'$.

  $$ A_{\text{rectangle}} = 5' \times 6' = 30 , \text{square feet} $$

• Area of the triangle: The base is $2'$ and the height is $4'$.

  $$ A_{\text{triangle}} = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 2' \times 4' = 4 , \text{square feet} $$

4. Add the areas together for figure b

Combine the areas of the rectangle and triangle:

$$ A_{\text{total_b}} = A_{\text{rectangle}} + A_{\text{triangle}} = 30 , \text{square feet} + 4 , \text{square feet} = 34 , \text{square feet} $$