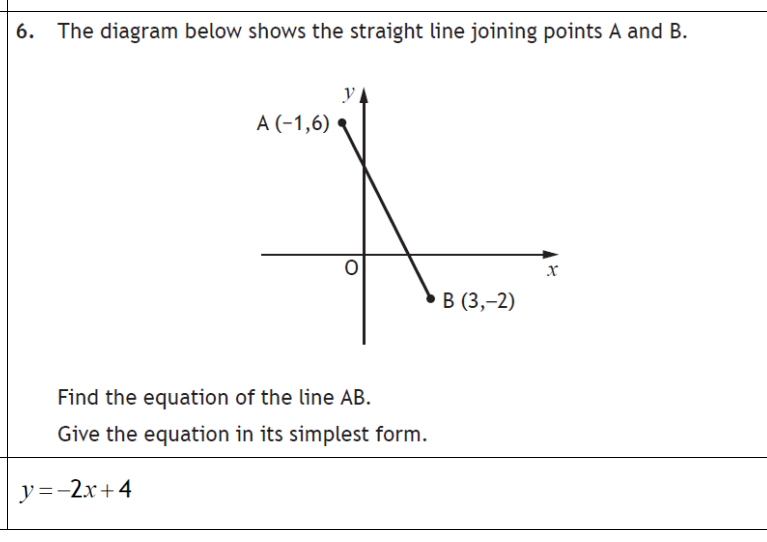
Find the equation of the line AB, given points A(-1, 6) and B(3, -2). Give the equation in its simplest form.
Understand the Problem
The question asks to find the equation of a straight line AB, given the coordinates of two points A and B. The final answer should be in its simplest form. The provided solution y = -2x + 4 is incorrect, we need to provide step by step working to arrive at the correct solution.
Answer
$y = -2x + 4$
Answer for screen readers
$y = -2x + 4$
Steps to Solve
-
Calculate the gradient (m) The gradient of a line passing through two points $(x_1, y_1)$ and $(x_2, y_2)$ is given by the formula: $m = \frac{y_2 - y_1}{x_2 - x_1}$. Given A(-1, 6) and B(3, -2), we have: $m = \frac{-2 - 6}{3 - (-1)} = \frac{-8}{4} = -2$
-
Use the point-slope form of a linear equation The point-slope form of a linear equation is $y - y_1 = m(x - x_1)$. We can use either point A or point B. Let's use point A(-1, 6). $y - 6 = -2(x - (-1))$ $y - 6 = -2(x + 1)$
-
Simplify the equation to slope-intercept form (y = mx + c) Expand and rearrange the equation: $y - 6 = -2x - 2$ $y = -2x - 2 + 6$ $y = -2x + 4$
$y = -2x + 4$
More Information
The equation of the line AB is $y = -2x + 4$. This is in the slope-intercept form, where the slope is -2 and the y-intercept is 4.
Tips
A common mistake is incorrectly calculating the gradient or making a sign error when substituting the coordinates into the point-slope form. Another common mistake is not simplifying the equation to its simplest form. Always double-check your calculations and make sure the equation is in the required format.
AI-generated content may contain errors. Please verify critical information