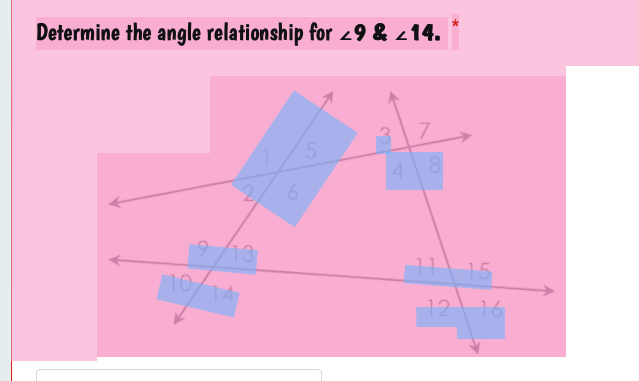
Determine the angle relationship for ∠9 & ∠14.

Understand the Problem

The question is asking us to identify the relationship between angles labeled 9 and 14 in a diagram involving intersecting lines. This likely involves concepts such as corresponding angles, alternate interior angles, or supplementary angles.

Answer

Angles $ \angle 9 $ and $ \angle 14 $ are alternate interior angles.

Steps to Solve

Identify the Intersection Point

In the diagram, lines intersect, creating pairs of angles. Angle 9 is on one line and angle 14 is formed by the intersection of another line crossing through it.
Analyze the Position of Angles

Angle 9 is either an alternate interior angle or a corresponding angle to angle 14, depending on their respective positioning about the intersecting transversal line.
Determine the Angle Relationship

If angles 9 and 14 are on opposite sides of the transversal and within the parallel lines, then they are classified as alternate interior angles. If they occupy the same relative position, they are corresponding angles.
Conclude the Relationship

Since angle 9 and angle 14 are positioned in such a way that they lie between the two parallel lines and are on opposite sides of the transversal, the relationship is:

$$ \angle 9 \text{ and } \angle 14 \text{ are alternate interior angles.} $$

The relationship is that angles ( \angle 9 ) and ( \angle 14 ) are alternate interior angles.

More Information

Alternate interior angles are equal when two parallel lines are crossed by a transversal. This principle is often used in geometry for proofs and solving problems involving parallel lines.

Tips

Misidentifying the angles based on their location. Ensure you're looking at the correct transversal and the corresponding parallel lines.
Confusing alternate interior with corresponding angles. Remember, corresponding angles occupy the same relative position at every intersection.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!