Determine M_O. (Round the final answers to four decimal places. Include a minus sign if necessary.)
Understand the Problem
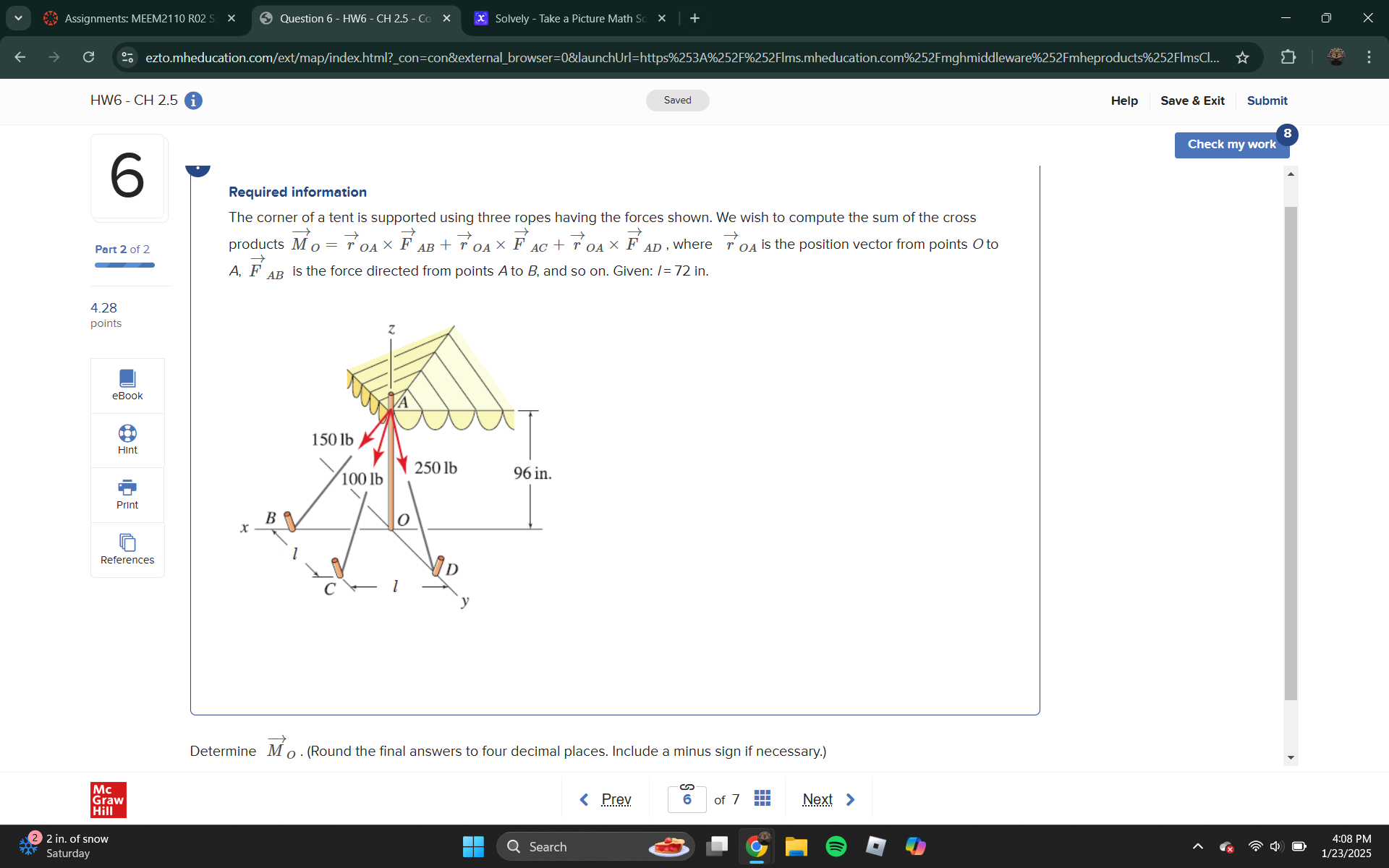
The question is asking to compute the sum of the cross products involving forces acting on a framework supported by ropes, along with the position vector from points O to A. It involves applying principles of static equilibrium and vector operations in physics.
Answer
The final result for \( \vec{M}_O \) needs to be computed but follows the outlined steps for calculation.
Answer for screen readers
The computed value of ( \vec{M}_O ) rounded to four decimal places is ( \vec{M}_O = \begin{bmatrix} M_x \ M_y \ M_z \end{bmatrix} ) lb-in, where ( M_x, M_y, M_z ) are the resultant values from the calculations.
Steps to Solve
- Identify Forces and Convert Units
Identify the forces acting at point O and convert any units to a consistent system (e.g., pounds to inches or feet). The forces are:
- ( \vec{F}_{AB} = 150 , \text{lb} )
- ( \vec{F}_{AC} = 100 , \text{lb} )
- ( \vec{F}_{AD} = 250 , \text{lb} )
- Determine Position Vectors
Calculate the position vectors from point O to points A, B, C, and D using given dimensions. The position vector ( \vec{r}_{OA} ) is typically noted as:
$$ \vec{r}_{OA} = \begin{bmatrix} 0 \ 0 \ 96 \end{bmatrix} , \text{in} $$
- Calculate Cross Products
Use the formula for the cross product, ( \vec{u} \times \vec{v} ). For each pair of vectors (position and force), compute:
- ( \vec{r}{OA} \times \vec{F}{AB} )
- ( \vec{r}{OA} \times \vec{F}{AC} )
- ( \vec{r}{OA} \times \vec{F}{AD} )
This requires the determinant of a 3x3 matrix:
$$ \vec{r} \times \vec{F} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \ x_1 & y_1 & z_1 \ x_2 & y_2 & z_2 \end{vmatrix} $$ for each calculation.
- Sum the Cross Products
Combine the results of the three cross products calculated in the previous step:
$$ \vec{M}O = \vec{r}{OA} \times \vec{F}{AB} + \vec{r}{OA} \times \vec{F}{AC} + \vec{r}{OA} \times \vec{F}_{AD} $$
- Calculate and Round the Final Result
Compute the final numerical results for ( \vec{M}_O ) and round to four decimal places, ensuring to include a minus sign if necessary.
The computed value of ( \vec{M}_O ) rounded to four decimal places is ( \vec{M}_O = \begin{bmatrix} M_x \ M_y \ M_z \end{bmatrix} ) lb-in, where ( M_x, M_y, M_z ) are the resultant values from the calculations.
More Information
The final answer will represent the moment about point O due to the forces acting on the framework. This is important in structural analysis to ensure that the framework can sustain the applied loads without collapsing.
Tips
- Incorrect Unit Conversion: Always ensure units are consistent before calculations.
- Misapplication of Cross Product: Check the determinant setup; it's easy to misorder coordinates or omit terms.
- Forgetting to Sum Moments: It’s crucial to sum all components of the cross products correctly.
AI-generated content may contain errors. Please verify critical information