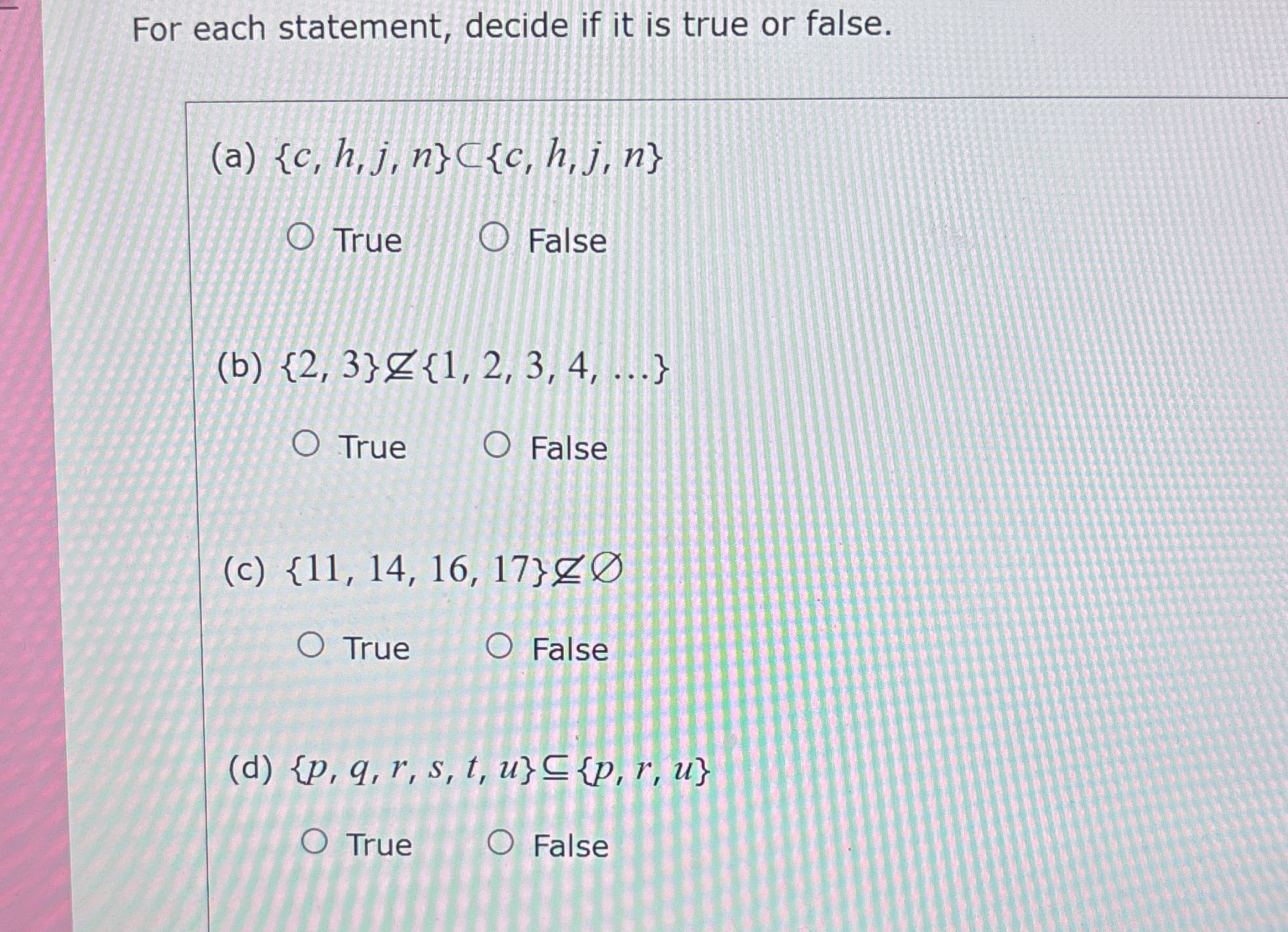
Determine if the following statements are true or false: (a) {c, h, j, n} ⊂ {c, h, j, n} (b) {2, 3} ⊈ {1, 2, 3, 4, ...} (c) {11, 14, 16, 17} ⊉ ∅ (d) {p, q, r, s, t, u} ⊆ {p, r, u} Determine if the following statements are true or false: (a) {c, h, j, n} ⊂ {c, h, j, n} (b) {2, 3} ⊈ {1, 2, 3, 4, ...} (c) {11, 14, 16, 17} ⊉ ∅ (d) {p, q, r, s, t, u} ⊆ {p, r, u}
Understand the Problem
The question presents four statements involving set theory and asks to determine whether each statement is true or false. Understanding the definitions of subset, proper subset, and the empty set is crucial to answering this question.
Answer
(a) False (b) False (c) False (d) False
Answer for screen readers
(a) False (b) False (c) False (d) False
Steps to Solve
-
Statement (a): {c, h, j, n} ⊂ {c, h, j, n} The symbol ⊂ denotes a proper subset. A proper subset means that all elements of the first set are in the second set, but the two sets are not equal. Since the two sets are equal, the statement is false.
-
Statement (b): {2, 3} ⊈ {1, 2, 3, 4, ...} The symbol ⊈ means "is not a subset of". Since both 2 and 3 are elements of {1, 2, 3, 4, ...}, {2, 3} is a subset of {1, 2, 3, 4, ...}. Therefore the statement is false.
-
Statement (c): {11, 14, 16, 17} ⊉ ∅ The symbol ⊉ means "is not a superset of". The empty set ∅ is a subset of every set. Therefore, any set is a superset of the empty set, so {11, 14, 16, 17} contains the empty set. Thus, the statement is false.
-
Statement (d): {p, q, r, s, t, u} ⊆ {p, r, u} The symbol ⊆ denotes a subset. For the first set to be a subset of the second set, all elements of the first set must be in the second set. However, q, s, and t are in {p, q, r, s, t, u} but not in {p, r, u}. Therefore, the statement is false.
(a) False (b) False (c) False (d) False
More Information
In set theory:
- A set $A$ is a subset of a set $B$ if every element of $A$ is also an element of $B$. We denote this as $A \subseteq B$.
- A set $A$ is a proper subset of a set $B$ if $A \subseteq B$ and $A \ne B$. We denote this as $A \subset B$.
- If $A$ is a subset of $B$, then $B$ is a superset of $A$, denoted as $B \supseteq A$.
- If $A$ is a proper subset of $B$, then $B$ is a proper superset of $A$, denoted as $B \supset A$.
- The empty set, denoted by $\emptyset$ or ${}$, is a subset of every set.
Tips
A common mistake is confusing the subset and proper subset symbols. Also, students sometimes forget that the empty set is a subset of every set.
AI-generated content may contain errors. Please verify critical information