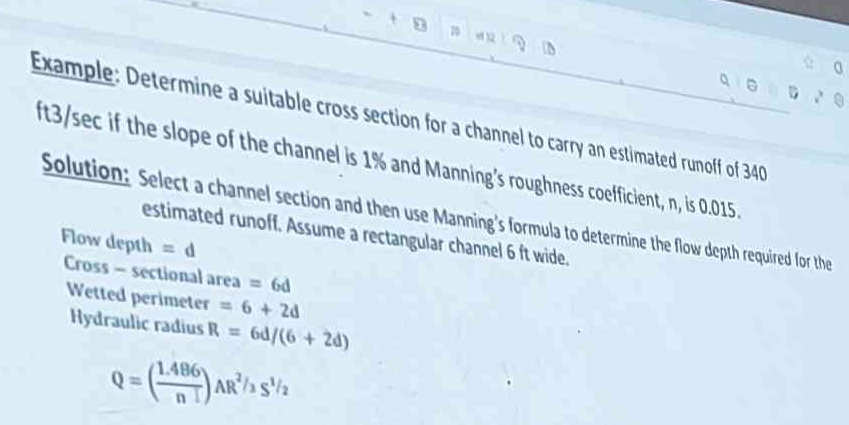
Determine a suitable cross section for a channel to carry an estimated runoff of 340 ft^3/sec if the slope of the channel is 1% and Manning's roughness coefficient, n, is 0.015. Se... Determine a suitable cross section for a channel to carry an estimated runoff of 340 ft^3/sec if the slope of the channel is 1% and Manning's roughness coefficient, n, is 0.015. Select a channel section and then use Manning's formula to determine the flow depth required for the estimated runoff. Assume a rectangular channel 6 ft wide. Read more

Steps to Solve

1. State Manning's Formula

Manning's formula is given as: $Q = \left(\frac{1.486}{n}\right) A R^{2/3} S^{1/2}$

2. Define the known values

From the problem statement we know the following: $Q = 340 , \text{ft}^3/\text{sec}$ $n = 0.015$ $S = 1% = 0.01$ Channel width $= 6 , \text{ft}$

3. Define Area, Wetted Perimeter, and Hydraulic Radius

The problem also provides the formulas for area, wetted perimeter, and hydraulic radius: $A = 6d$ $P = 6 + 2d$ $R = \frac{6d}{6 + 2d}$

4. Substitute known values into Manning's Formula

Substitute all known values into Manning's formula: $340 = \left(\frac{1.486}{0.015}\right) (6d) \left(\frac{6d}{6 + 2d}\right)^{2/3} (0.01)^{1/2}$

5. Simplify the equation

Simplify $ \left(\frac{1.486}{0.015}\right)$ and $(0.01)^{1/2}$: $\left(\frac{1.486}{0.015}\right) \approx 99.07$ $(0.01)^{1/2} = 0.1$

Substitute these values into the equation: $340 = (99.07) (6d) \left(\frac{6d}{6 + 2d}\right)^{2/3} (0.1)$ $340 = 59.442 d \left(\frac{6d}{6 + 2d}\right)^{2/3}$

6. Isolate the term with $d$

Divide both sides by $59.442$: $\frac{340}{59.442} = d \left(\frac{6d}{6 + 2d}\right)^{2/3}$ $5.72 = d \left(\frac{6d}{6 + 2d}\right)^{2/3}$

7. Solve for $d$ numerically

This equation is difficult to solve analytically, so we will solve numerically by guessing and checking or using software. By either method, the solution is approximately:

$d \approx 2.5 , \text{ft}$