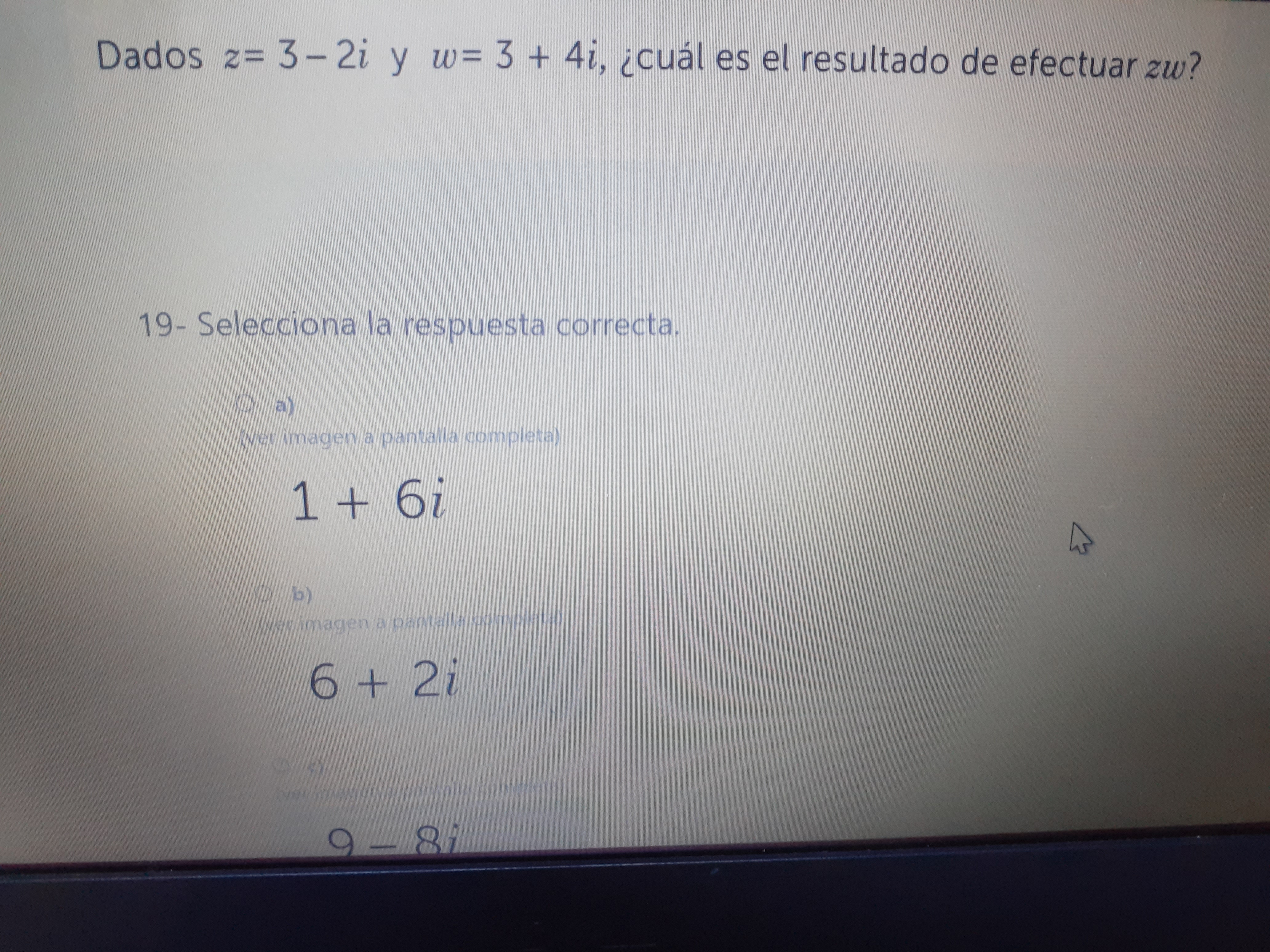
Dados z=3-2i y w=3+4i, ¿cuál es el resultado de efectuar zw?
Understand the Problem
La pregunta es para determinar cual es el resultado de multiplicar dos números complejos, z y w. z = 3-2i y w = 3 + 4i, así que necesitamos calcular el producto zw.
Answer
$17 + 6i$
Answer for screen readers
$17 + 6i$
Steps to Solve
- Escribir la expresión para multiplicar
Escribimos la multiplicación de los dos números complejos:
$zw = (3 - 2i)(3 + 4i)$
- Expandir el producto
Expandimos el producto usando la propiedad distributiva (FOIL):
$zw = 3(3) + 3(4i) - 2i(3) - 2i(4i)$ $zw = 9 + 12i - 6i - 8i^2$
- Simplificar la expresión
Simplificamos la expresión, recordando que $i^2 = -1$:
$zw = 9 + 6i - 8(-1)$ $zw = 9 + 6i + 8$
- Combinar los términos reales
Combinamos los términos reales:
$zw = 17 + 6i$
$17 + 6i$
More Information
El producto de los números complejos $z=3-2i$ y $w=3+4i$ es $17 + 6i$.
Tips
Un error común al multiplicar números complejos es olvidar que $i^2 = -1$. Otro error es equivocarse al aplicar la propiedad distributiva (FOIL).
AI-generated content may contain errors. Please verify critical information