Dados $z = -2 + 3i$ y $w = 4 + 2i$, ¿cuál es el resultado de efectuar $\frac{z}{w}$?
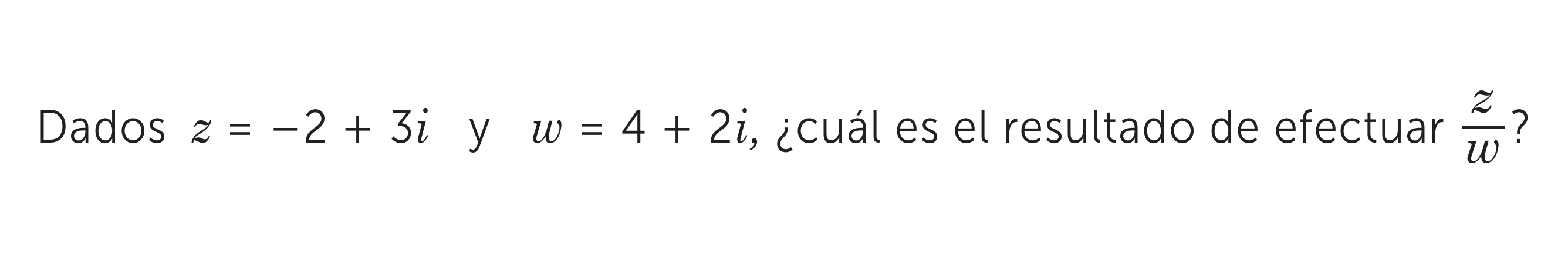
Understand the Problem
La pregunta es sobre números complejos. Nos dan dos números complejos, z y w, y nos piden calcular el resultado de la división z/w. Esto implica realizar la división de los dos números complejos y simplificar el resultado a la forma a + bi, donde a y b son números reales.
Answer
$$ -\frac{1}{10} + \frac{4}{5}i $$
Answer for screen readers
$$ -\frac{1}{10} + \frac{4}{5}i $$
Steps to Solve
- Escribir la división Escribimos la división de los números complejos $z$ y $w$ como una fracción:
$$ \frac{z}{w} = \frac{-2 + 3i}{4 + 2i} $$
- Multiplicar por el conjugado Para dividir números complejos, multiplicamos el numerador y el denominador por el conjugado del denominador. El conjugado de $4 + 2i$ es $4 - 2i$.
$$ \frac{-2 + 3i}{4 + 2i} \cdot \frac{4 - 2i}{4 - 2i} $$
- Expandir el numerador Multiplicamos los términos en el numerador:
$$ (-2 + 3i)(4 - 2i) = -2(4) -2(-2i) + 3i(4) + 3i(-2i) = -8 + 4i + 12i - 6i^2 $$ Dado que $i^2 = -1$, tenemos: $$ -8 + 16i - 6(-1) = -8 + 16i + 6 = -2 + 16i $$
- Expandir el denominador Multiplicamos los términos en el denominador:
$$ (4 + 2i)(4 - 2i) = 4(4) + 4(-2i) + 2i(4) + 2i(-2i) = 16 - 8i + 8i - 4i^2 $$ Dado que $i^2 = -1$, tenemos: $$ 16 - 4(-1) = 16 + 4 = 20 $$
- Escribir la fracción resultante Juntamos el numerador y el denominador calculados:
$$ \frac{-2 + 16i}{20} $$
- Simplificar la fracción Dividimos cada término en el numerador por el denominador:
$$ \frac{-2}{20} + \frac{16i}{20} = -\frac{1}{10} + \frac{4}{5}i $$
$$ -\frac{1}{10} + \frac{4}{5}i $$
More Information
El resultado de dividir los dos números complejos $z$ y $w$ es un nuevo número complejo. La parte real es $-\frac{1}{10}$ y la parte imaginaria es $\frac{4}{5}$.
Tips
- Olvidar multiplicar tanto el numerador como el denominador por el conjugado.
- Errores al expandir los productos en el numerador y el denominador.
- Olvidar que $i^2 = -1$.
- No simplificar la fracción al final.
AI-generated content may contain errors. Please verify critical information