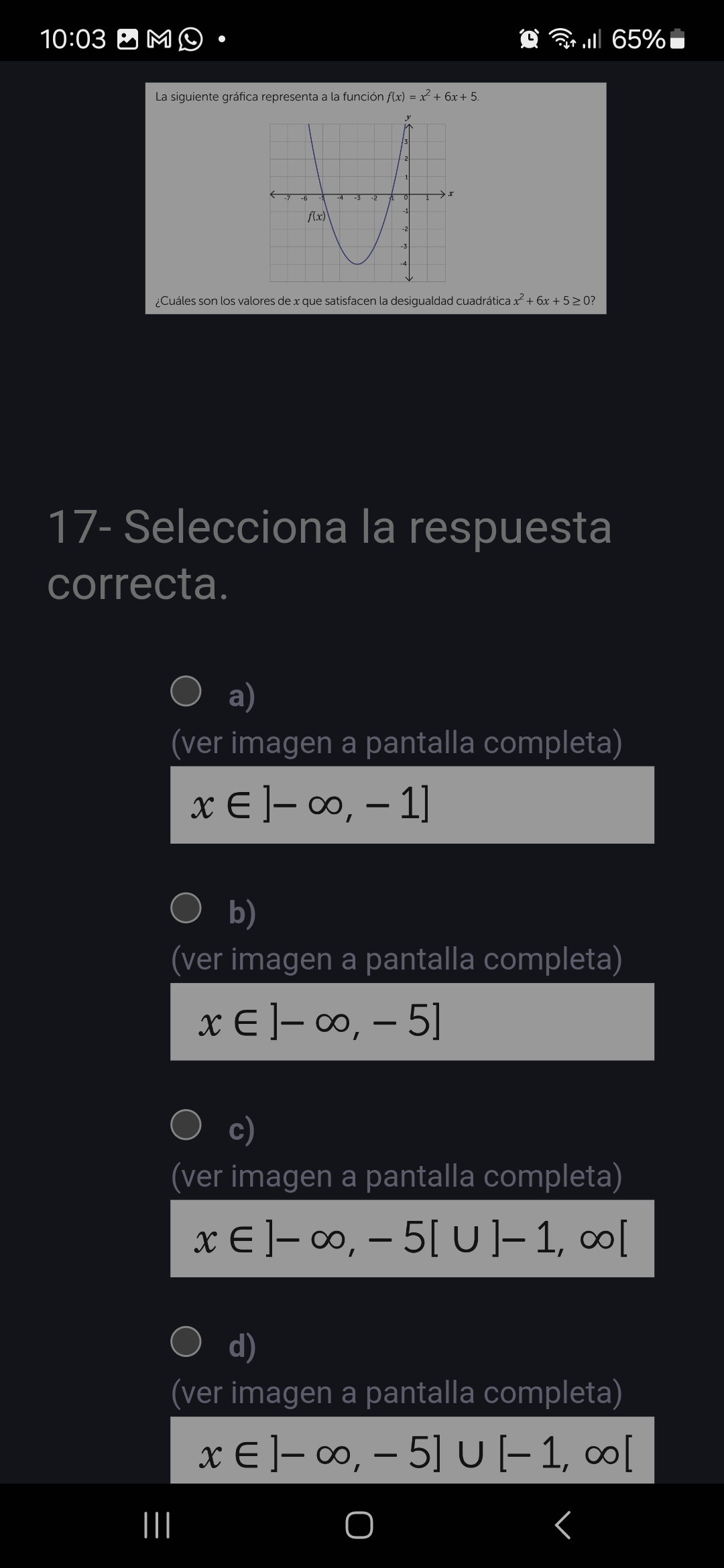
¿Cuáles son los valores de x que satisfacen la desigualdad cuadrática x² + 6x + 5 ≥ 0?
Understand the Problem
La pregunta presenta una función cuadrática graficada, f(x) = x² + 6x + 5, y pide determinar los valores de x que satisfacen la desigualdad cuadrática x² + 6x + 5 ≥ 0. En otras palabras, se busca el rango de valores de x para los cuales la función es mayor o igual a cero.
Answer
$x \in (-\infty, -5] \cup [-1, \infty)$
Answer for screen readers
$x \in (-\infty, -5] \cup [-1, \infty)$
Steps to Solve
- Identify the x-intercepts of the function
From the graph, we can see that the parabola intersects the x-axis at $x = -5$ and $x = -1$. These are the roots of the quadratic equation $x^2 + 6x + 5 = 0$.
- Determine the intervals where the function is non-negative
We want to find the values of $x$ for which $x^2 + 6x + 5 \geq 0$. This means we are looking for the intervals where the graph of the function is above or on the x-axis.
- Express the solution as a union of intervals
The parabola is above or on the x-axis for $x \leq -5$ and $x \geq -1$. Therefore, the solution to the inequality is $x \in (-\infty, -5] \cup [-1, \infty)$. Note that we include the points $x = -5$ and $x = -1$ because the inequality is greater than or equal to zero.
$x \in (-\infty, -5] \cup [-1, \infty)$
More Information
The solution represents all real numbers less than or equal to -5, and all real numbers greater than or equal to -1.
Tips
A common mistake is to only consider the interval between the roots, or to incorrectly state whether the endpoints should be included or excluded. Remember to consider both regions outside the roots when the parabola opens upwards and the question asks for greater than or equal to zero. Also, pay attention to whether the inequality is strict ($>$ or $<$) or non-strict ($\geq$ or $\leq$) to determine if the roots should be included in the solution.
AI-generated content may contain errors. Please verify critical information