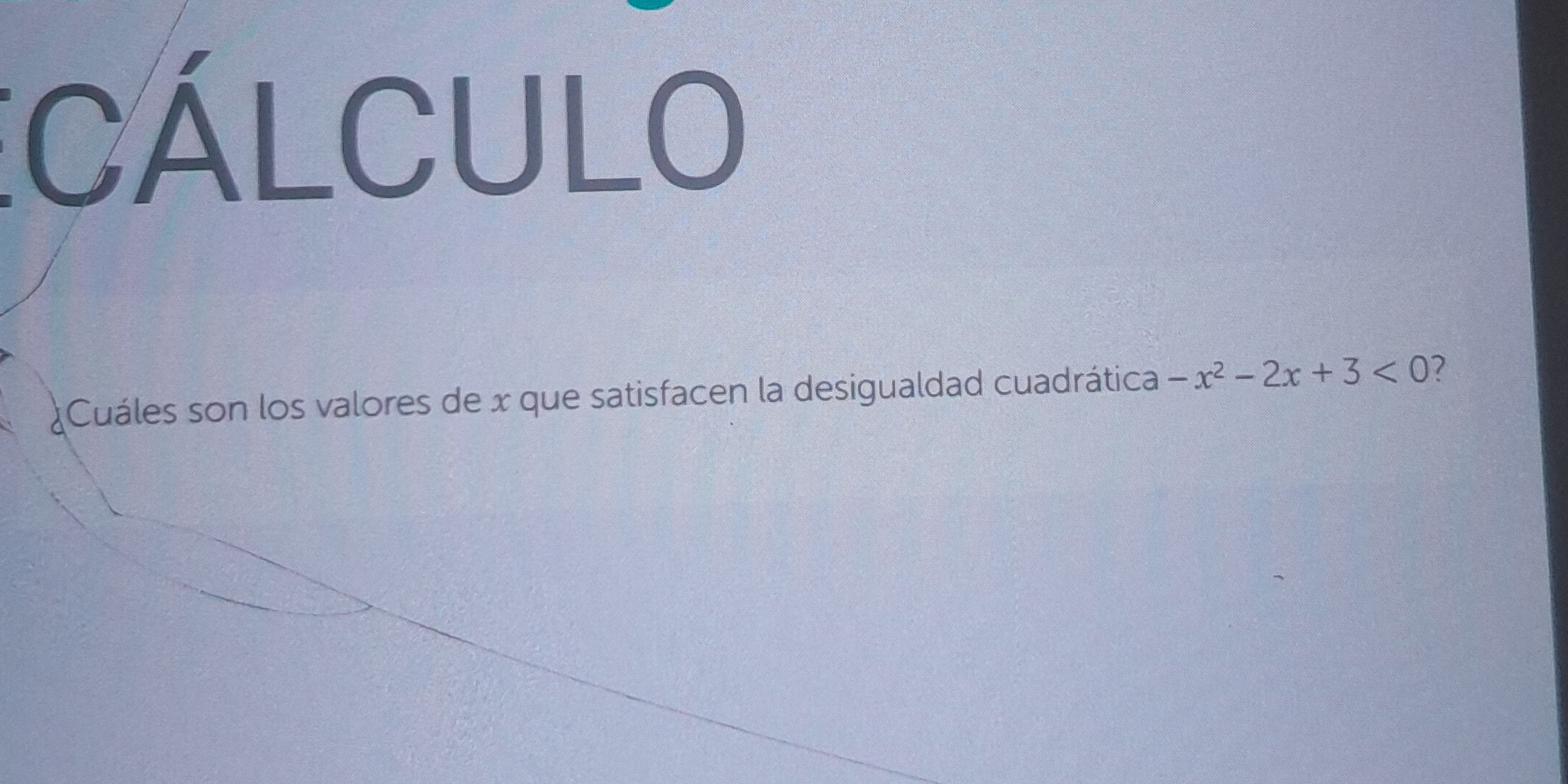
¿Cuáles son los valores de x que satisfacen la desigualdad cuadrática -x² - 2x + 3 < 0?
Understand the Problem
La pregunta te pide encontrar los valores de 'x' que cumplen con la desigualdad cuadrática dada, que es -x² - 2x + 3 < 0. Para resolver esto, podrías seguir estos pasos: primero, intentar factorizar la expresión cuadrática o usar la fórmula cuadrática para encontrar las raíces. Luego, analiza los intervalos definidos por estas raíces para determinar dónde la desigualdad es verdadera.
Answer
$x < -3$ o $x > 1$
Answer for screen readers
$x < -3$ o $x > 1$
Steps to Solve
- Multiplicar por -1
Multiplicamos ambos lados de la inecuación por -1. Esto cambia la dirección de la desigualdad:
$$ -x^2 - 2x + 3 < 0 $$ $$ x^2 + 2x - 3 > 0 $$
- Factorizar la expresión cuadrática
Factorizamos el lado izquierdo de la desigualdad:
$$ (x+3)(x-1) > 0 $$
- Encontrar los puntos críticos
Los puntos críticos son los valores de $x$ que hacen $(x+3)(x-1) = 0$. Éstos son $x = -3$ y $x = 1$.
- Probar los intervalos
Los puntos críticos dividen la recta numérica en tres intervalos: $(-\infty, -3)$, $(-3, 1)$, y $(1, \infty)$. Probamos un valor de prueba de cada intervalo en la desigualdad original $x^2 + 2x - 3 > 0$ para ver si cumple con la condición.
-
Para $(-\infty, -3)$, usemos $x = -4$: $(-4+3)(-4-1) = (-1)(-5) = 5 > 0$. Así que este intervalo satisface la desigualdad.
-
Para $(-3, 1)$, usemos $x = 0$: $(0+3)(0-1) = (3)(-1) = -3 < 0$. Así que este intervalo no satisface la desigualdad.
-
Para $(1, \infty)$, usemos $x = 2$: $(2+3)(2-1) = (5)(1) = 5 > 0$. Así que este intervalo satisface la desigualdad.
- Escribir la solución
La desigualdad se cumple para $x < -3$ o $x > 1$.
$x < -3$ o $x > 1$
More Information
La solución representa todos los valores de $x$ que hacen que la expresión cuadrática $-x^2 - 2x + 3$ sea menor que cero. Estos valores se encuentran fuera del intervalo entre las raíces de la ecuación cuadrática.
Tips
Un error común es olvidar cambiar la dirección de la desigualdad al multiplicar o dividir por un número negativo. En este caso, al multiplicar la desigualdad original por -1, es crucial recordar invertir el signo de la desigualdad. Otro error común ocurre al no probar los puntos críticos en la desigualdad original. Asegúrate de que los extremos de los intervalos abiertos no estén incluidos en la solución si la desigualdad es estricta (< o >).
AI-generated content may contain errors. Please verify critical information