¿Cuál triángulo rectángulo cumple con que la razón tan θ = 3/2?
Understand the Problem
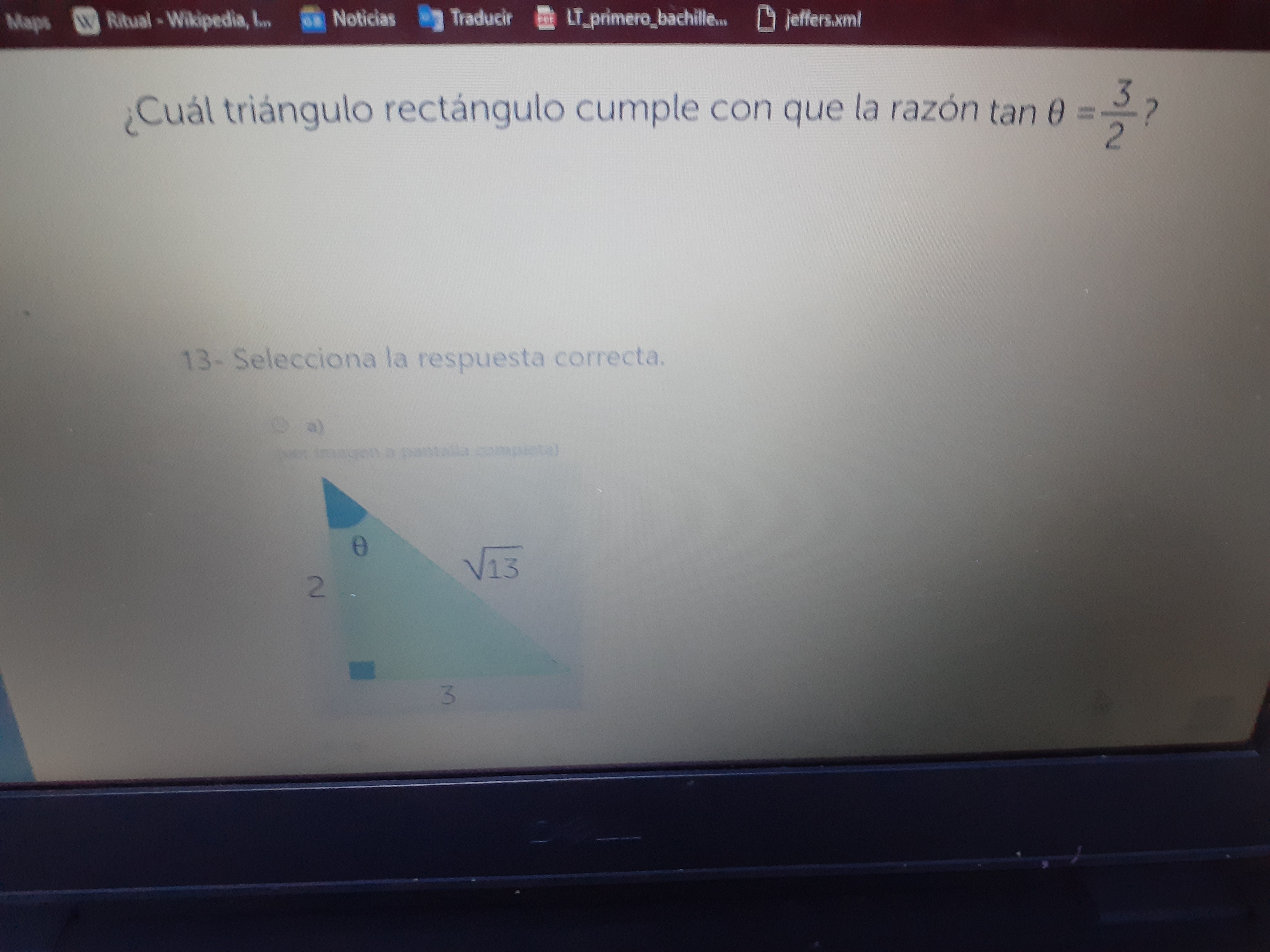
La pregunta pide identificar cuál triángulo rectángulo cumple con la condición de que la tangente del ángulo θ sea igual a 3/2. Esto implica verificar las relaciones entre los lados del triángulo (cateto opuesto y cateto adyacente) con respecto al ángulo θ.
Answer
The triangle in the image satisfies the condition $\tan \theta = \frac{3}{2}$.
Answer for screen readers
The triangle shown satisfies the condition $\tan \theta = \frac{3}{2}$.
Steps to Solve
- Recall the definition of tangent
The tangent of an angle $\theta$ in a right triangle is defined as the ratio of the length of the side opposite to the angle to the length of the side adjacent to the angle. $$ \tan \theta = \frac{\text{opposite}}{\text{adjacent}} $$
- Analyze the given triangle
In the given triangle, the side opposite to angle $\theta$ has a length of 3, and the side adjacent to angle $\theta$ has a length of 2.
- Calculate the tangent of $\theta$ for the given triangle $$ \tan \theta = \frac{3}{2} $$
The triangle shown satisfies the condition $\tan \theta = \frac{3}{2}$.
More Information
The tangent function relates angles to the ratio of sides in right triangles, and it's a fundamental concept in trigonometry.
Tips
Null
AI-generated content may contain errors. Please verify critical information