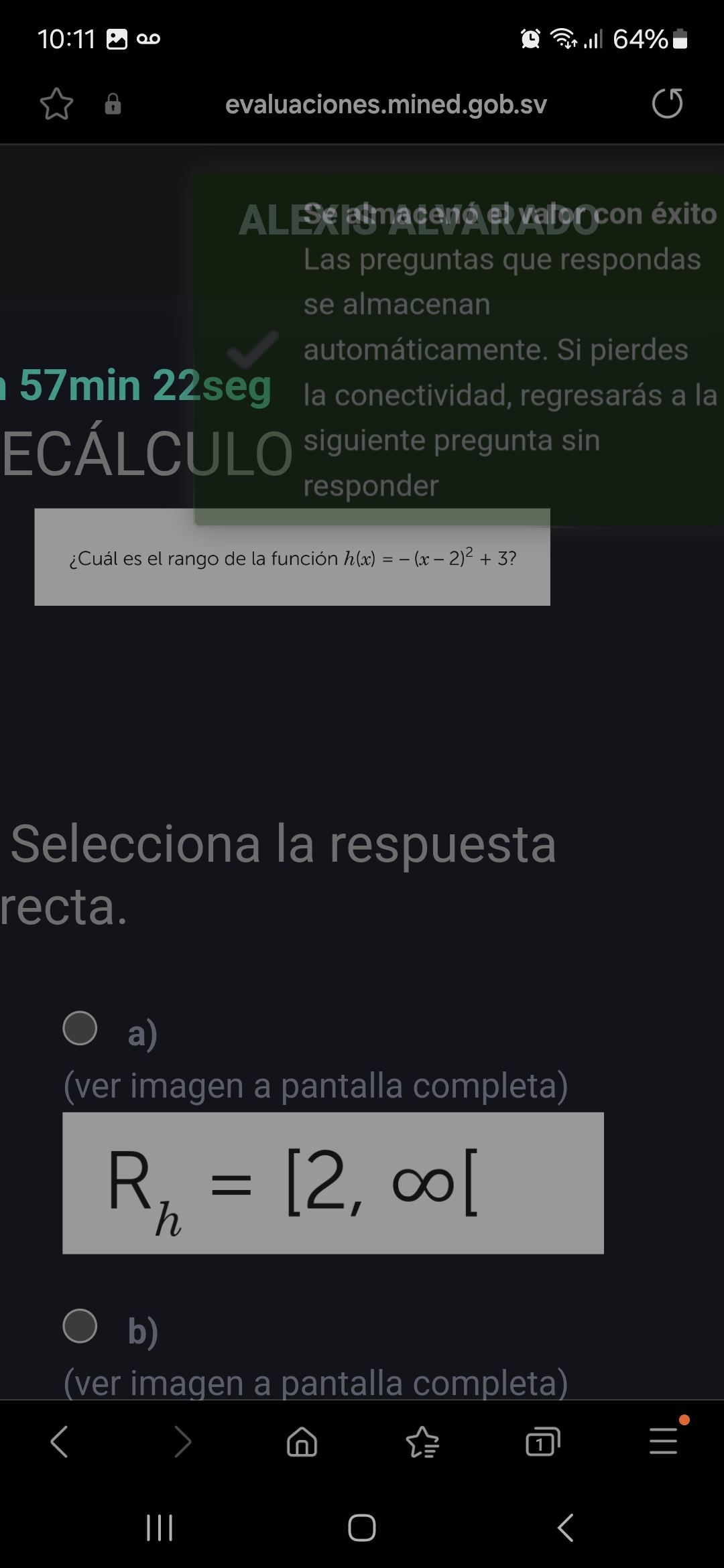
¿Cuál es el rango de la función h(x) = -(x-2)^2 + 3?
Understand the Problem
La pregunta solicita determinar el rango de la función cuadrática dada. La función es h(x) = -(x-2)^2 + 3. Para encontrar el rango, necesitamos considerar el vértice de la parábola y la dirección en que se abre. Como el coeficiente principal es negativo, la parábola se abre hacia abajo, lo que significa que el vértice será el punto máximo.
Answer
$(-\infty, 3]$
Answer for screen readers
$(-\infty, 3]$
Steps to Solve
- Identificar la forma de la función
La función $h(x) = -(x - 2)^2 + 3$ está en forma de vértice.
- Determinar el vértice de la parábola
El vértice de la parábola está dado por $(h, k)$, donde $h(x) = a(x - h)^2 + k$. En este caso, $h = 2$ y $k = 3$. Por tanto, el vértice es $(2, 3)$.
- Determinar la dirección en que se abre la parábola
Dado que el coeficiente principal es negativo ($-1$), la parábola se abre hacia abajo.
- Determinar el rango
Como la parábola se abre hacia abajo y el vértice es $(2, 3)$, el valor máximo de la función es 3. Por lo tanto, el rango de la función es $(-\infty, 3]$.
$(-\infty, 3]$
More Information
El rango representa todos los posibles valores de salida de la función. En este caso, debido a que la parábola se abre hacia abajo, el valor máximo que alcanza la función es 3, y todos los valores menores a 3 también están incluidos en el rango.
Tips
Un error común es confundir el rango con el dominio. El dominio de esta función es todos los números reales, pero el rango está limitado por el valor máximo de la parábola. Otro error común es utilizar el vértice incorrectamente o no considerar la dirección de la parábola.
AI-generated content may contain errors. Please verify critical information