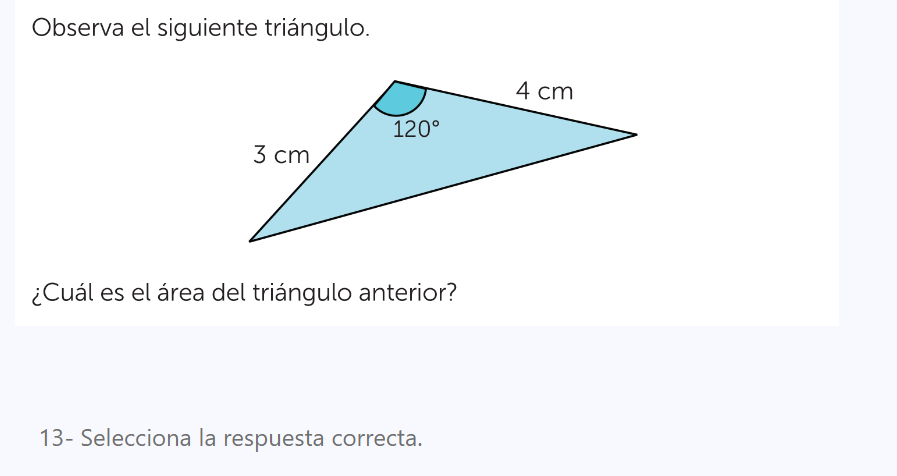
¿Cuál es el área del triángulo anterior?
Understand the Problem
La pregunta está pidiendo calcular el área de un triángulo dado, utilizando las medidas de sus lados y un ángulo.
Answer
El área del triángulo es $3\sqrt{3} \, \text{cm}^2$.
Answer for screen readers
El área del triángulo es $3\sqrt{3} , \text{cm}^2$.
Steps to Solve
- Identificar los datos del triángulo
En el triángulo se tiene un lado de 3 cm, un lado de 4 cm y un ángulo de 120°. Estos son los datos necesarios para calcular el área.
- Usar la fórmula del área de un triángulo
Para calcular el área de un triángulo con dos lados y el ángulo entre ellos, usamos la fórmula:
$$ A = \frac{1}{2} \cdot a \cdot b \cdot \sin(C) $$
donde $a$ y $b$ son los longitudes de los lados (3 cm y 4 cm), y $C$ es el ángulo entre ellos (120°).
- Sustituir los valores en la fórmula
Sustituyendo los valores en la fórmula del área:
$$ A = \frac{1}{2} \cdot 3 \cdot 4 \cdot \sin(120°) $$
- Calcular el valor de $\sin(120°)$
Para calcular el área, necesitamos evaluar $\sin(120°)$. Sabemos que:
$$ \sin(120°) = \sin(180° - 60°) = \sin(60°) = \frac{\sqrt{3}}{2} $$
- Completar el cálculo del área
Sustituyendo $\sin(120°)$ en la fórmula de área:
$$ A = \frac{1}{2} \cdot 3 \cdot 4 \cdot \frac{\sqrt{3}}{2} $$
- Simplificar la expresión
Realizamos la multiplicación y simplificación:
$$ A = \frac{1}{2} \cdot 3 \cdot 4 \cdot \frac{\sqrt{3}}{2} = \frac{12\sqrt{3}}{4} = 3\sqrt{3} $$
El área del triángulo es $3\sqrt{3} , \text{cm}^2$.
More Information
El área se obtiene utilizando la fórmula común para triángulos que involucra dos lados y el ángulo entre ellos. El uso de la función seno permite incluir la medida del ángulo en el cálculo.
Tips
- Confundir los ángulos: Asegúrate de usar el ángulo correcto entre los dos lados.
- Errores en cálculo de seno: Verifica que estés usando la función seno de manera correcta, especialmente con ángulos obtusos.
AI-generated content may contain errors. Please verify critical information