Simplify: (-4 \sqrt[3]{29}) \cdot (-3 \sqrt[3]{38})
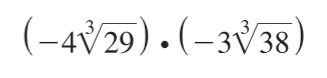
Understand the Problem
The question requires multiplying two expressions, each containing a cube root. We need to simplify this expression by multiplying the coefficients and the cube roots together.
Answer
$12\sqrt[3]{1102}$
Answer for screen readers
$12\sqrt[3]{1102}$
Steps to Solve
- Multiply the coefficients
Multiply the numbers outside the cube roots: $(-4) \cdot (-3) = 12$
- Multiply the cube roots
Multiply the numbers inside the cube roots: $\sqrt[3]{29} \cdot \sqrt[3]{38} = \sqrt[3]{29 \cdot 38} = \sqrt[3]{1102}$
- Combine the results
Combine the result from step 1 and step 2: $12\sqrt[3]{1102}$
$12\sqrt[3]{1102}$
More Information
The cube root of 1102 cannot be simplified further, as 1102 does not have any perfect cube factors.
Tips
A common mistake would be to multiply the coefficients with the numbers inside the cube roots. Remember to keep coefficients separate from the numbers inside the radicals until the radicals are simplified or multiplied.
AI-generated content may contain errors. Please verify critical information