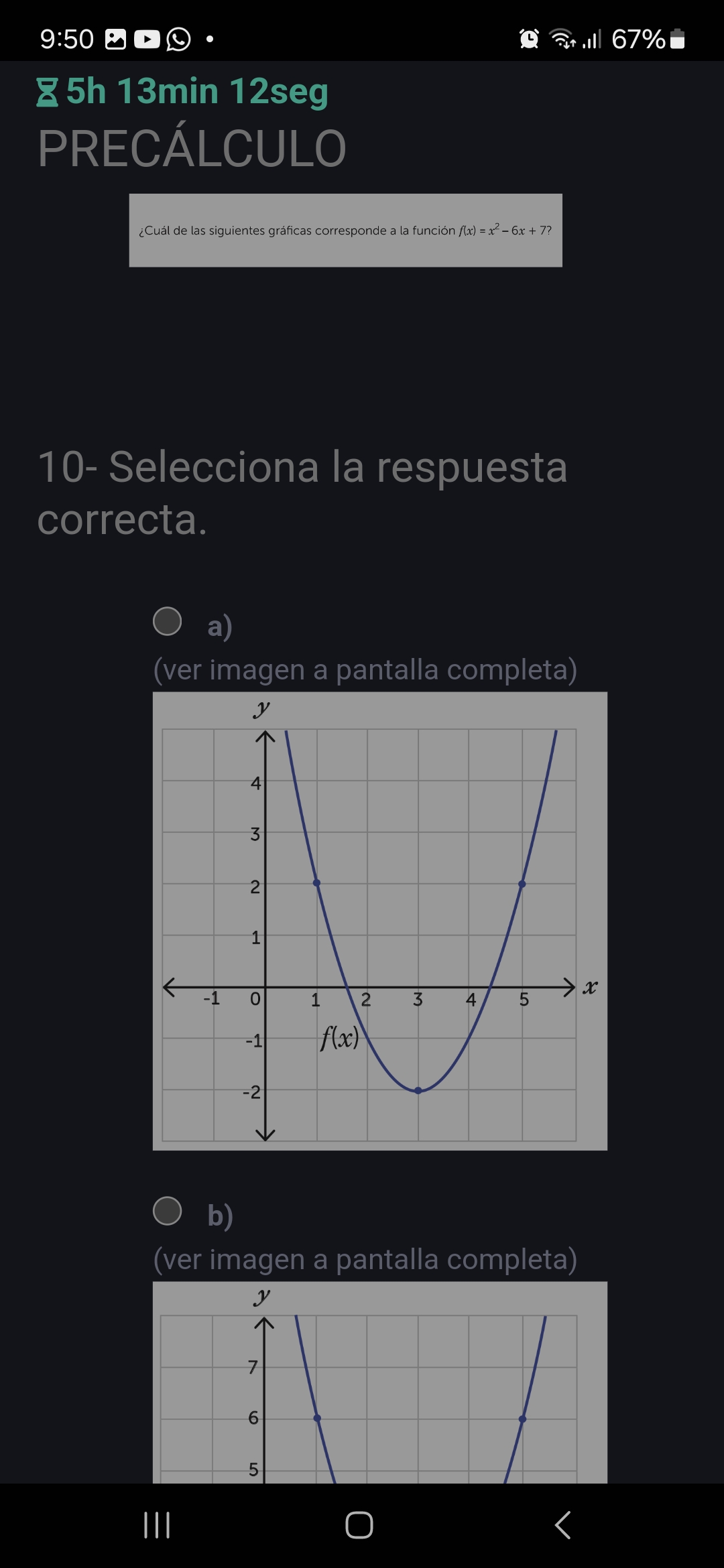
¿Cuál de las siguientes gráficas corresponde a la función f(x) = x² - 6x + 7?
Understand the Problem
La pregunta te pide identificar cuál de las gráficas corresponde a la función cuadrática dada f(x) = x² - 6x + 7. Para resolver esto, puedes analizar las propiedades de la función, como el vértice, la concavidad y las intersecciones con los ejes, y compararlas con las gráficas proporcionadas.
Answer
a)
Answer for screen readers
a)
Steps to Solve
- Find the vertex of the parabola
The x-coordinate of the vertex can be found using the formula $x = -\frac{b}{2a}$, where $a$ and $b$ are the coefficients of the quadratic equation $ax^2 + bx + c = 0$.
In this case, $f(x) = x^2 - 6x + 7$, so $a = 1$ and $b = -6$.
$$ x = -\frac{-6}{2(1)} = \frac{6}{2} = 3 $$
Now, find the y-coordinate of the vertex by plugging $x = 3$ into the function:
$$ f(3) = (3)^2 - 6(3) + 7 = 9 - 18 + 7 = -2 $$
So, the vertex of the parabola is at $(3, -2)$.
- Determine the concavity & y-intercept
Since the coefficient of the $x^2$ term is positive ($a = 1 > 0$), the parabola opens upwards (concave up).
To find the y-intercept, set $x = 0$ in the equation:
$$ f(0) = (0)^2 - 6(0) + 7 = 7 $$
So, the y-intercept is at $(0, 7)$.
- Identify the correct graph
We are looking for a parabola that opens upwards, has a vertex at $(3, -2)$, and a y-intercept at $(0, 7)$. Looking at the provided images, graph 'a' has a vertex at $(3, -2)$ and opens upward.
a)
More Information
The vertex of a parabola is the minimum or maximum point on the graph. The y-intercept is the point at which the graph crosses the y-axis.
Tips
null
AI-generated content may contain errors. Please verify critical information