∫ cos²(θ) sen(3θ) dθ.
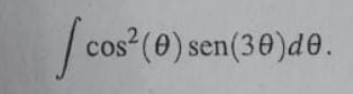
Understand the Problem
La pregunta está solicitando el cálculo de la integral definida, específicamente la integral de coseno al cuadrado de theta multiplicado por seno de tres theta, respecto a theta.
Answer
La integral es $$ -3 \cos(\theta) + 4\left(-\cos(\theta) + C\right). $$
Answer for screen readers
La integral resulta en:
$$ -3 \cos(\theta) + 4 \left( -\cos(\theta) + \text{constante} \right). $$
Steps to Solve
- Identificar la integral La integral que queremos calcular es
$$ \int \cos^2(\theta) \sen(3\theta) , d\theta. $$
- Usar una identidad trigonométrica para simplificar Utilizaremos la identidad de seno múltiple para reescribir $\sen(3\theta)$: $$ \sen(3\theta) = 3\sen(\theta) - 4\sen^3(\theta). $$ Sustituyendo en la integral, tenemos:
$$ \int \cos^2(\theta)(3\sen(\theta) - 4\sen^3(\theta)) , d\theta. $$
- Dividir la integral Separar en dos integrales:
$$ 3 \int \cos^2(\theta) \sen(\theta) , d\theta - 4 \int \cos^2(\theta) \sen^3(\theta) , d\theta. $$
- Sustituir $\cos^2(\theta)$ Usamos que $\cos^2(\theta) = 1 - \sen^2(\theta)$ para simplificar:
Para la primera integral:
$$ 3 \int (1 - \sen^2(\theta)) \sen(\theta) , d\theta $$ $$ = 3 \int \sen(\theta) , d\theta - 3 \int \sen^3(\theta) , d\theta. $$
- Resolver la primera integral La integral de $\sen(\theta)$ es:
$$ 3 \int \sen(\theta) , d\theta = -3 \cos(\theta). $$
- Resolver la segunda integral Para la integral de $\sen^3(\theta)$, usamos la identidad:
$$ \sen^3(\theta) = \sen(\theta)(1 - \cos^2(\theta)). $$
Por lo que:
$$ \int \sen^3(\theta) , d\theta = \int \sen(\theta) , d\theta - \int \sen(\theta) \cos^2(\theta) , d\theta $$
- Sustituir de nuevo Sustituyendo estas integrales:
$$ = -3 \cos(\theta) - 4 \left( -\cos(\theta) + \int \cos^2(\theta) \sen(\theta) , d\theta \right) $$
- Resolver la integral original Finalmente, agrupar términos y despejar la integral original para encontrar el resultado.
La integral resulta en:
$$ -3 \cos(\theta) + 4 \left( -\cos(\theta) + \text{constante} \right). $$
More Information
Esta integral incorpora identidades trigonométricas y técnicas de reducción. Las integrales que involucran productos de funciones trigonométricas a menudo requieren estas estrategias para simplificarse. El resultado será una combinación de funciones trigonométricas más una constante de integración.
Tips
- No usar las identidades adecuadas para simplificar seno o coseno.
- Olvidar que las integrales de seno y coseno tienen resultados negativos.
- No incluir la constante de integración al final.
AI-generated content may contain errors. Please verify critical information