Consider the following piecewise function f(x), where A and B are constants. Determine all values of the constants A and B so that limit as x approaches -2 of f(x) and limit as x... Consider the following piecewise function f(x), where A and B are constants. Determine all values of the constants A and B so that limit as x approaches -2 of f(x) and limit as x approaches 1 of f(x) both exist.
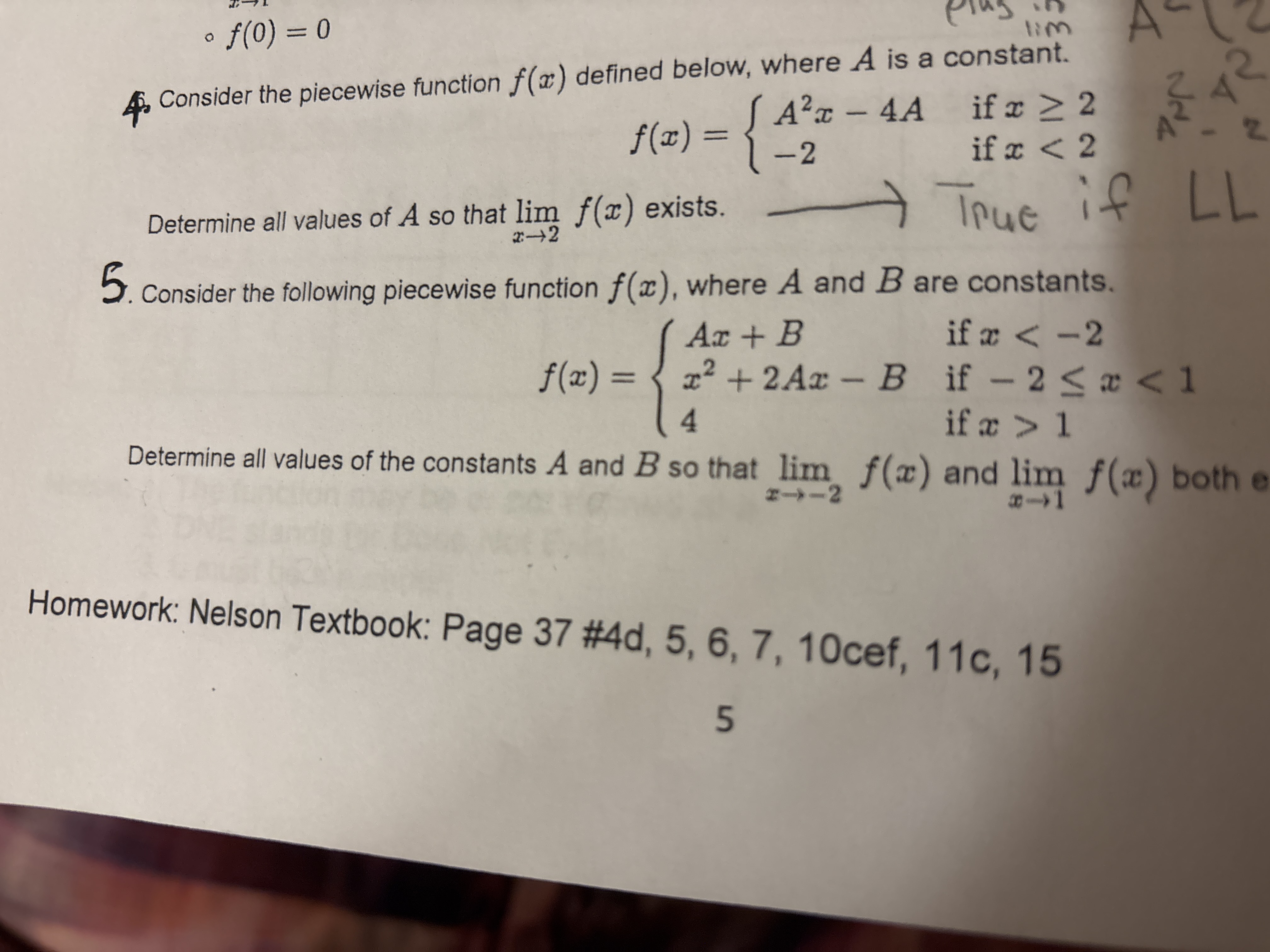
Understand the Problem
The question asks us to determine the values of constants A and B such that the limits of a piecewise function f(x) exist as x approaches -2 and 1.
Answer
$A = \frac{5}{3}$, $B = \frac{1}{3}$
Answer for screen readers
$A = \frac{5}{3}$ and $B = \frac{1}{3}$
Steps to Solve
- Limit as $x$ approaches -2
To find the limit as $x$ approaches $-2$, we need to ensure the left-hand limit (LHL) and the right-hand limit (RHL) are equal. The LHL is given by the first case, $Ax + B$, and the RHL is given by the second case, $x^2 + 2Ax - B$. So, we have:
$$ \lim_{x \to -2^-} f(x) = A(-2) + B = -2A + B $$
$$ \lim_{x \to -2^+} f(x) = (-2)^2 + 2A(-2) - B = 4 - 4A - B $$
For the limit to exist at $x = -2$, we must have:
$$ -2A + B = 4 - 4A - B $$
Simplifying the above equation we get: $$ 2A + 2B = 4 $$ $$ A + B = 2 $$
- Limit as $x$ approaches 1
Similarly, for the limit as $x$ approaches $1$ to exist, the LHL and RHL must be equal. The LHL is given by the second case, $x^2 + 2Ax - B$, and the RHL is given by the third case, $4$. So we have:
$$ \lim_{x \to 1^-} f(x) = (1)^2 + 2A(1) - B = 1 + 2A - B $$
$$ \lim_{x \to 1^+} f(x) = 4 $$
For the limit to exist at $x=1$, we must have:
$$ 1 + 2A - B = 4 $$
Simplifying the above equation we get:
$$ 2A - B = 3 $$
- Solving for A and B
We now have a system of two linear questions:
$$ A + B = 2 $$
$$ 2A - B = 3 $$
Adding both equations, we have:
$$ 3A = 5 $$ $$ A = \frac{5}{3} $$
Substituting A back into $A + B = 2$, we get:
$$ \frac{5}{3} + B = 2 $$
$$ B = 2 - \frac{5}{3} $$ $$ B = \frac{6}{3} - \frac{5}{3} $$ $$ B = \frac{1}{3} $$
$A = \frac{5}{3}$ and $B = \frac{1}{3}$
More Information
The solution ensures the piecewise function has limits at the transition points $x = -2$ and $x = 1$ by equating the left-hand and right-hand limits at those points and solving the resulting system of equations.
Tips
A common mistake is not ensuring that both the left-hand limit and right-hand limit are equal at the transition points. Another mistake may be in solving the simultaneous equations obtained after equating the limits.
AI-generated content may contain errors. Please verify critical information