Calcule a integral: ∫ (x²)/((x - 3)(x² + 2)) dx.
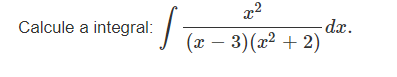
Understand the Problem
La pregunta está pidiendo calcular la integral definida de una función racional. Para resolverlo, utilizaremos técnicas de integración, como la descomposición en fracciones parciales.
Answer
$$ \int \frac{x^2}{(x-3)(x^2+2)}dx = \frac{9}{11} \ln|x - 3| + \frac{1}{11} \ln|x^{2} + 2| + \frac{6}{11\sqrt{2}} \tan^{-1}\left(\frac{x}{\sqrt{2}}\right) + C $$
Answer for screen readers
La integral es:
$$ \int \frac{x^2}{(x-3)(x^2+2)}dx = \frac{9}{11} \ln|x - 3| + \frac{1}{11} \ln|x^{2} + 2| + \frac{6}{11\sqrt{2}} \tan^{-1}\left(\frac{x}{\sqrt{2}}\right) + C $$
Steps to Solve
- Descomposición en fracciones parciales
Para integrar la función $\frac{x^{2}}{(x - 3)(x^{2} + 2)}$, comenzamos descomponiéndola en fracciones parciales. Queremos encontrar constantes $A$, $B$ y $C$ tales que:
$$ \frac{x^{2}}{(x - 3)(x^{2} + 2)} = \frac{A}{x - 3} + \frac{Bx + C}{x^{2} + 2} $$
Multiplicamos ambos lados por el denominador $\ (x - 3)(x^{2} + 2)$ para despejar la fracción:
$$ x^{2} = A(x^{2} + 2) + (Bx + C)(x - 3) $$
- Expandir y simplificar
Expandimos la ecuación resultante:
$$ x^{2} = Ax^{2} + 2A + Bx^{2} - 3Bx + Cx - 3C $$
Agrupamos términos semejantes:
$$ x^{2} = (A + B)x^{2} + (-3B + C)x + (2A - 3C) $$
- Igualar coeficientes
Igualamos los coeficientes de ambos lados de la ecuación:
- Para $x^{2}$: $A + B = 1$
- Para $x$: $-3B + C = 0$
- Para términos constantes: $2A - 3C = 0$
- Resolver el sistema de ecuaciones
Ahora tenemos un sistema de ecuaciones:
- $A + B = 1$
- $-3B + C = 0$
- $2A - 3C = 0$
Sustituyendo $C = 3B$ en la tercera ecuación:
$$ 2A - 3(3B) = 0 \implies 2A - 9B = 0 \implies A = \frac{9}{2}B $$
Sustituyendo esto en $A + B = 1$:
$$ \frac{9}{2}B + B = 1 \implies \frac{11}{2}B = 1 \implies B = \frac{2}{11} $$
Luego, $A = 1 - B = 1 - \frac{2}{11} = \frac{9}{11}$
Y finalmente, $C = 3B = 3(\frac{2}{11}) = \frac{6}{11}$
- Sustitución en fracciones parciales
Sustituyendo $A$, $B$ y $C$ en la descomposición original:
$$ \frac{x^{2}}{(x - 3)(x^{2} + 2)} = \frac{9/11}{x - 3} + \frac{(2/11)x + (6/11)}{x^{2} + 2} $$
- Integrar cada término por separado
Ahora integramos cada una de las fracciones:
$$ \int \left(\frac{9/11}{x - 3}\right)dx + \int \left(\frac{(2/11)x + (6/11)}{x^{2} + 2}\right)dx $$
El primer término se integra como:
$$ \frac{9}{11} \ln|x - 3| $$
Para el segundo término, separamos la fracción:
$$ \int \frac{(2/11)x}{x^{2} + 2}dx + \int \frac{(6/11)}{x^{2} + 2}dx $$
La primera parte se integra usando la regla de $u$-substitución, donde $u = x^{2} + 2 \implies du = 2xdx$:
$$ \int \frac{(2/11)x}{x^{2} + 2}dx = \frac{1}{11} \ln|x^{2} + 2| $$
La segunda parte es una integral más sencilla:
$$ \int \frac{(6/11)}{x^{2} + 2}dx = \frac{6}{11} \cdot \frac{1}{\sqrt{2}} \tan^{-1}\left(\frac{x}{\sqrt{2}}\right) $$
Reuniendo todas las partes, la integral definida es:
$$ \int \frac{x^2}{(x-3)(x^2+2)}dx = \frac{9}{11} \ln|x - 3| + \frac{1}{11} \ln|x^{2} + 2| + \frac{6}{11\sqrt{2}} \tan^{-1}\left(\frac{x}{\sqrt{2}}\right) + C $$
La integral es:
$$ \int \frac{x^2}{(x-3)(x^2+2)}dx = \frac{9}{11} \ln|x - 3| + \frac{1}{11} \ln|x^{2} + 2| + \frac{6}{11\sqrt{2}} \tan^{-1}\left(\frac{x}{\sqrt{2}}\right) + C $$
More Information
La solución fue obtenida mediante el uso de la descomposición en fracciones parciales y la integración de funciones racionales. Toma en cuenta que este tipo de integrales suelen aparecer en cálculo y es común utilizarlas en aplicaciones de física y matemáticas.
Tips
- Olvidar el signo en la integración: Asegúrate de incluir el signo correcto al integrar.
- No igualar correctamente los coeficientes: Verifica que los coeficientes estén correctamente escritos y iguales.
- Confundir la integración de $\tan^{-1}$: Asegúrate de recordar que $\int \frac{1}{a^2 + x^2}dx = \frac{1}{a} \tan^{-1}\left(\frac{x}{a}\right)$.
AI-generated content may contain errors. Please verify critical information