Solve for x: log₄x = -2.5
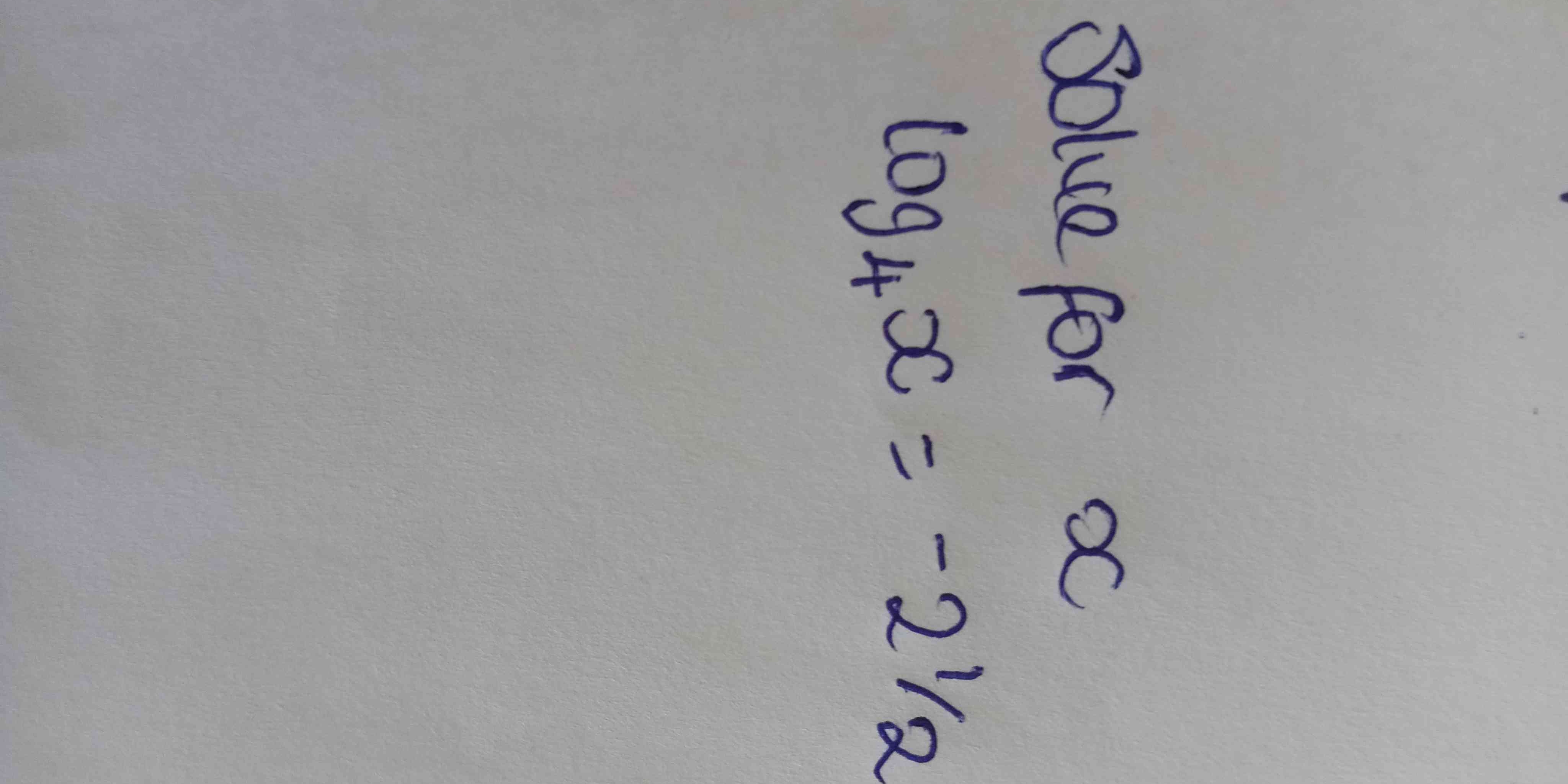
Understand the Problem
The question asks to find the value of 'x' in the logarithmic equation log₄x = -2.5. To solve this, we'll convert the logarithmic equation to its exponential form and then simplify to find the value of 'x'.
Answer
$x = \frac{1}{32}$
Answer for screen readers
$x = \frac{1}{32}$
Steps to Solve
- Convert the mixed number to a decimal
Convert $-2 \frac{1}{2}$ to a decimal.
$-2 \frac{1}{2} = -2.5$
So, the equation becomes:
$\log_4 x = -2.5$
- Convert the logarithmic equation to exponential form
The logarithmic equation $\log_b a = c$ is equivalent to the exponential equation $b^c = a$.
In our case, $\log_4 x = -2.5$, so $b = 4$, $c = -2.5$ and $a = x$. Therefore, the exponential form is:
$4^{-2.5} = x$
- Simplify the exponential expression
Rewrite $4$ as $2^2$ and $-2.5$ as $-\frac{5}{2}$
$x = 4^{-2.5} = (2^2)^{-\frac{5}{2}}$
Using the power of a power rule $(a^m)^n = a^{mn}$:
$x = 2^{2 \cdot (-\frac{5}{2})} = 2^{-5}$
- Calculate the final value of x
$x = 2^{-5} = \frac{1}{2^5} = \frac{1}{32}$
$x = \frac{1}{32}$
More Information
The value of $x$ that solves the equation $\log_4 x = -2.5$ is $\frac{1}{32}$.
Tips
A common mistake is incorrectly converting between logarithmic and exponential forms. Another mistake could be mishandling negative exponents or not simplifying the expression correctly.
AI-generated content may contain errors. Please verify critical information