Calculate the volume of oxygen produced at room temperature when a concentrated H2SO4 is electrolyzed for 30 min using a current.
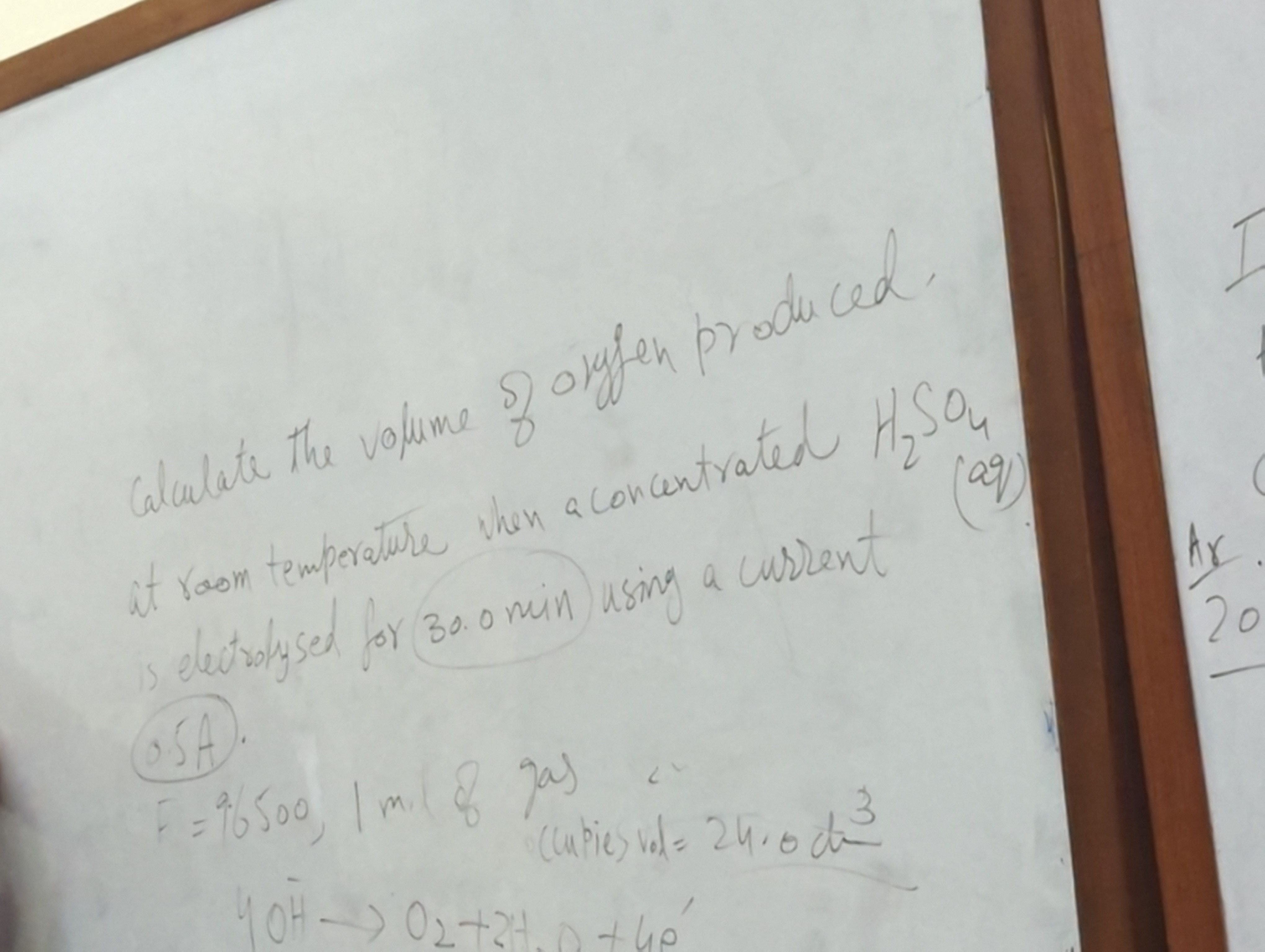
Understand the Problem
The question is asking to calculate the volume of oxygen produced during the electrolysis of concentrated sulfuric acid at room temperature over a specified duration using a current.
Answer
The volume of oxygen produced can be calculated as $V_{O₂} = n_{O₂} \times 24.0$.
Answer for screen readers
The volume of oxygen produced is $V_{O₂} , \text{(in dm}^3\text{)}$.
Steps to Solve
- Understand the Electrolysis Reaction
When concentrated sulfuric acid (H₂SO₄) undergoes electrolysis, water decomposition occurs, producing oxygen (O₂) at the anode. The balanced half-reaction for oxygen generation is: $$ 4OH^- \rightarrow 2H₂O + O₂ + 4e^- $$
- Determine the Quantity of Electric Charge (Coulombs)
Use the formula for electric charge: $$ Q = I \times t $$ Where:
- ( Q ) is the electric charge in coulombs (C)
- ( I ) is the current in amperes (A)
- ( t ) is time in seconds
Given ( t = 30.0 , \text{min} = 30.0 \times 60 , \text{s} = 1800 , \text{s} ).
- Calculate the Moles of Oxygen Produced
Using Faraday's laws, we find that 4 moles of electrons produce 1 mole of O₂:
- First, calculate the number of moles of electrons using Faraday's constant ( F \approx 96500 , \text{C/mol} ): $$ n = \frac{Q}{F} $$ Then, the moles of O₂ produced is: $$ n_{O₂} = \frac{n_{e^-}}{4} $$
- Convert Moles of Oxygen to Volume
At room temperature and 1 atm, the molar volume of a gas is approximately ( 24.0 , \text{dm}^3 ). The volume of oxygen produced is calculated as: $$ V_{O₂} = n_{O₂} \times 24.0 , \text{dm}^3 $$
The volume of oxygen produced is $V_{O₂} , \text{(in dm}^3\text{)}$.
More Information
The electrolysis of concentrated sulfuric acid primarily produces oxygen gas at the anode. The relationship between current, time, and volume is fundamental in electrochemical reactions.
Tips
- Not converting time into seconds properly before calculations.
- Forgetting to account for the stoichiometry in the half-reaction when calculating moles of oxygen.
AI-generated content may contain errors. Please verify critical information