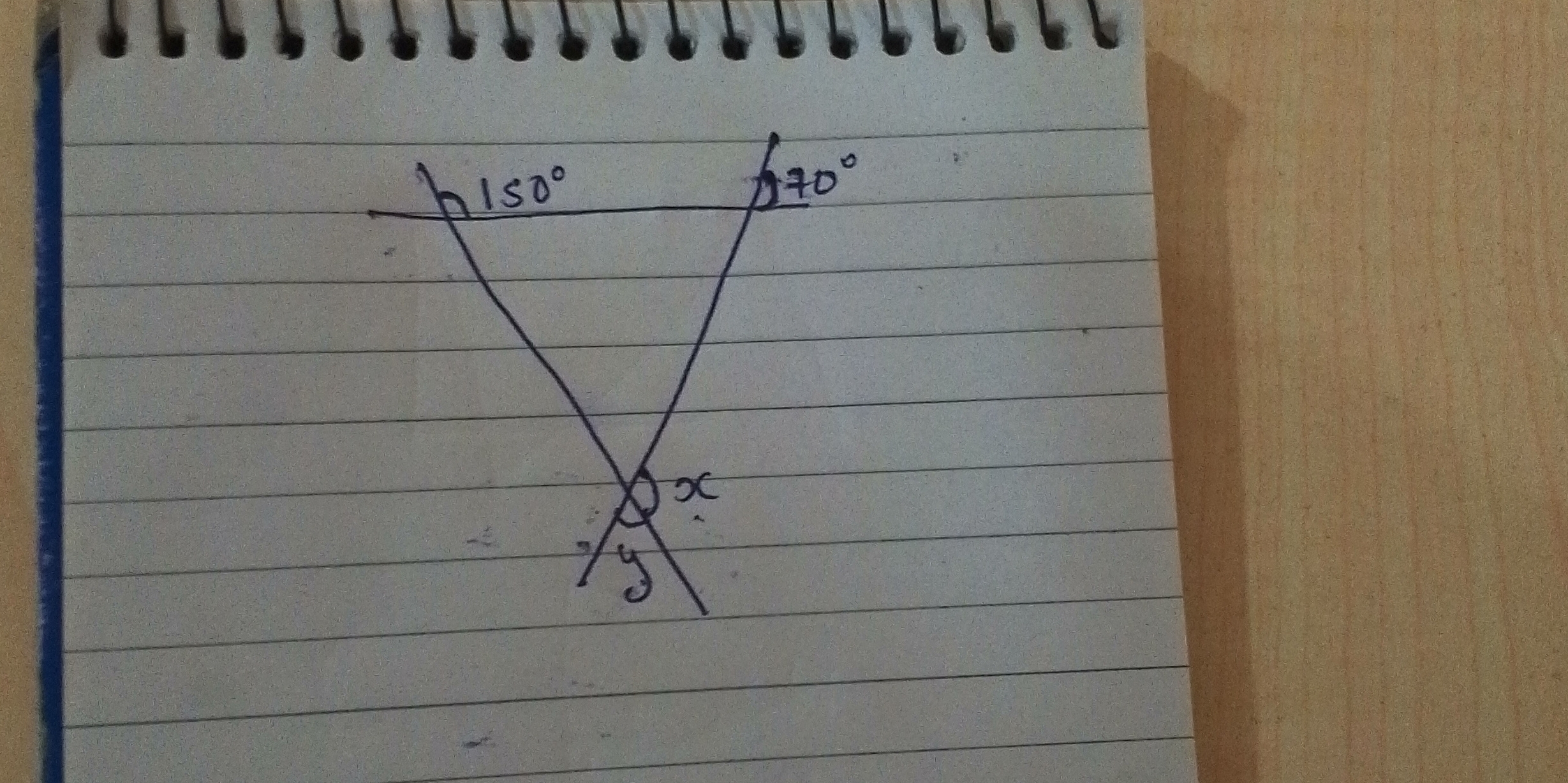
Find angles x and y.
Understand the Problem
The question asks us to find the values of angles x and y, given a diagram with some angles provided. The key understanding is that angles on a straight line add up to 180 degrees, and vertically opposite angles are equal.
Answer
$x = 40^\circ$ $y = 40^\circ$
Answer for screen readers
$x = 40^\circ$ $y = 40^\circ$
Steps to Solve
- Find the supplementary angle to $150^\circ$
Angles on a straight line add up to $180^\circ$. So, the angle adjacent to $150^\circ$ on the straight line is: $180^\circ - 150^\circ = 30^\circ$
- Find the supplementary angle to $70^\circ$
Similarly, the angle adjacent to $70^\circ$ on the straight line is: $180^\circ - 70^\circ = 110^\circ$
- Find angle $y$ using the triangle
In the triangle formed, the sum of angles is $180^\circ$. Thus, $y + 30^\circ + 110^\circ = 180^\circ$ $y + 140^\circ = 180^\circ$ $y = 180^\circ - 140^\circ = 40^\circ$
- Find angle $x$ using vertically opposite angles
Angle $x$ is vertically opposite to angle $y$, so they are equal. Therefore, $x = y = 40^\circ$
$x = 40^\circ$ $y = 40^\circ$
More Information
Vertically opposite angles are always equal. Supplementary angles add up to 180 degrees. The sum of internal angles in a triangle is also 180 degrees.
Tips
A common mistake is to assume that $x$ and $y$ are different, but in this case they are vertically opposite angles, hence they are equal. Another mistake might be incorrectly calculating the supplementary angles or the angles in the triangle by subtracting from values other than 180.
AI-generated content may contain errors. Please verify critical information