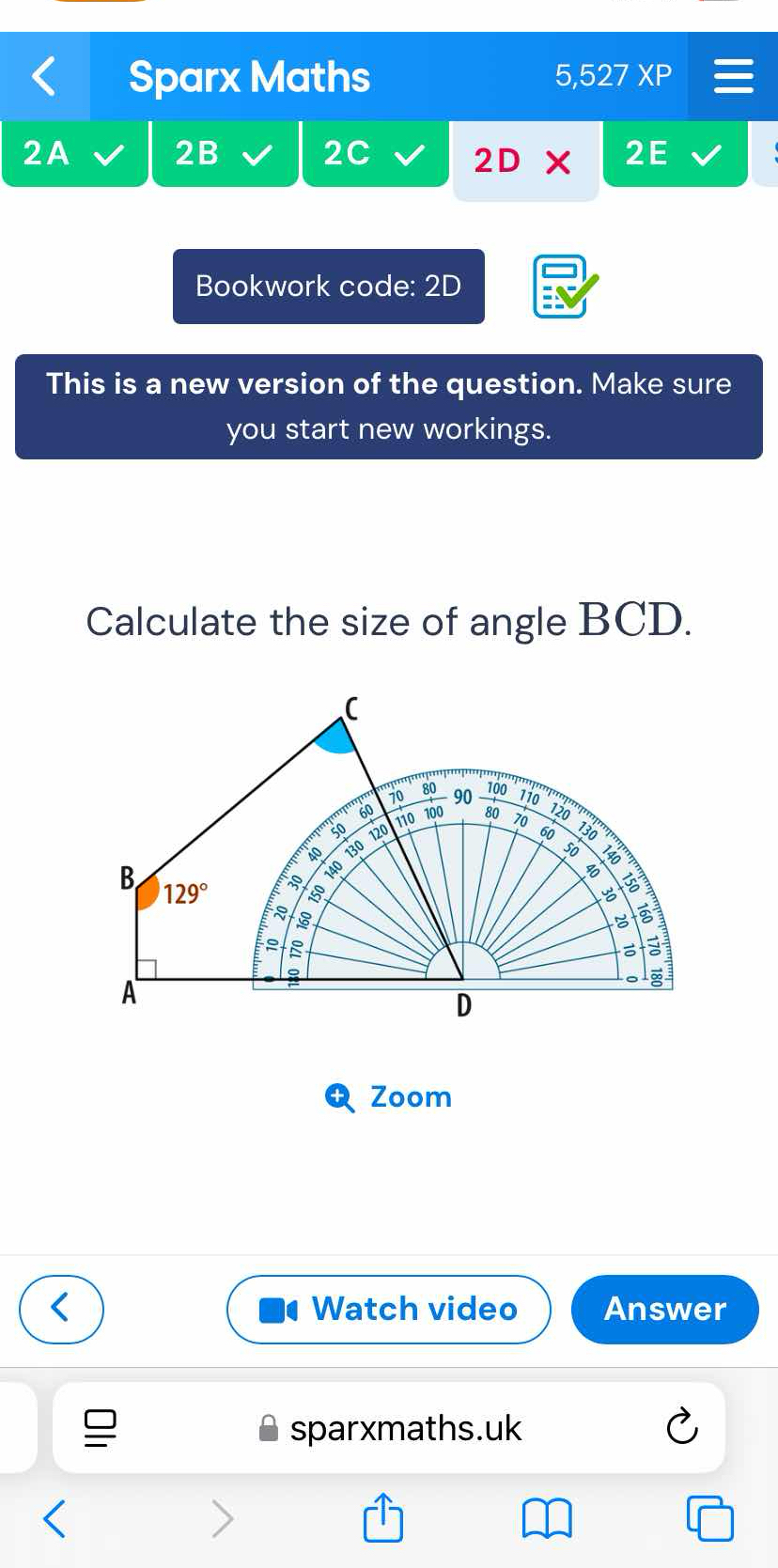
Calculate the size of angle BCD.
Understand the Problem
The question is asking for the calculation of angle BCD in a geometric setup where the angle ABC is given as 129°. To find angle BCD, we will need to use the fact that the sum of angles at point B should equal 180° since it forms a linear pair.
Answer
The angle BCD is $51^\circ$.
Answer for screen readers
The size of angle BCD is $51^\circ$.
Steps to Solve
- Identify the relationship between angles at point B
At point B, we know that angle ABC and angle BCD are supplementary, meaning they add up to 180°.
- Set up the equation
Given angle ABC = 129°, we can set up the equation:
$$ \text{Angle ABC} + \text{Angle BCD} = 180° $$
Substituting the known value:
$$ 129° + \text{Angle BCD} = 180° $$
- Solve for angle BCD
To find angle BCD, we need to isolate it in the equation. We can do this by subtracting 129° from both sides:
$$ \text{Angle BCD} = 180° - 129° $$
- Calculate angle BCD
Now, compute the subtraction:
$$ \text{Angle BCD} = 51° $$
The size of angle BCD is $51^\circ$.
More Information
Angle BCD is calculated using the property that the sum of the angles on a straight line is always 180°. This concept is fundamental in geometry and applies to any pair of supplementary angles.
Tips
- Forgetting the relationship: Some might forget that angles ABC and BCD together form a linear pair and must sum to 180°.
- Incorrect subtraction: Miscalculating the subtraction (e.g., writing 180° - 129° as 39° instead of the correct 51°).
AI-generated content may contain errors. Please verify critical information