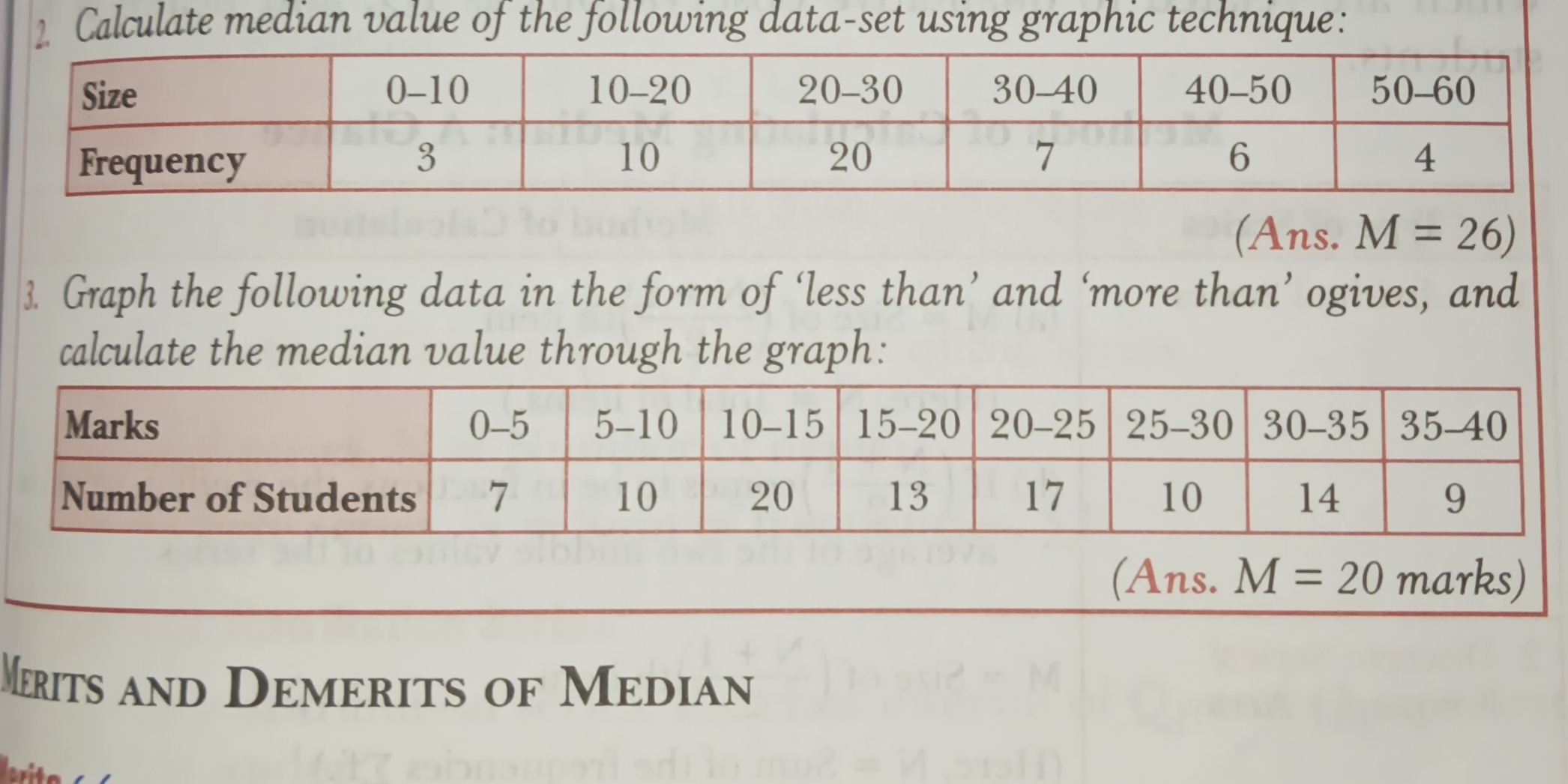
Calculate the median value of the following data-set using a graphic technique: Size: 0-10, 10-20, 20-30, 30-40, 40-50, 50-60 Frequency: 3, 10, 20, 7, 6, 4 Graph the following dat... Calculate the median value of the following data-set using a graphic technique: Size: 0-10, 10-20, 20-30, 30-40, 40-50, 50-60 Frequency: 3, 10, 20, 7, 6, 4 Graph the following data in the form of 'less than' and 'more than' ogives, and calculate the median value through the graph: Marks: 0-5, 5-10, 10-15, 15-20, 20-25, 25-30, 30-35, 35-40 Number of Students: 7, 10, 20, 13, 17, 10, 14, 9 Read more

Steps to Solve

1. Calculate cumulative frequencies for question 2

To find the median graphically, we first need to calculate the cumulative frequencies for the given data:

Size: 0-10, 10-20, 20-30, 30-40, 40-50, 50-60

Frequency: 3, 10, 20, 7, 6, 4

Cumulative Frequency (cf): 3, 13, 33, 40, 46, 50

2. Plot the "less than" ogive for question 2

The "less than" ogive is formed by plotting the upper limit of each class interval against its corresponding cumulative frequency.

Points to plot: (10, 3), (20, 13), (30, 33), (40, 40), (50, 46), (60, 50)

Draw a smooth curve through these points.

3. Determine the median position for question 2

The total frequency $N$ is 50. The median is the value corresponding to $N/2 = 50/2 = 25$.

4. Locate the median on the graph for question 2

Find 25 on the cumulative frequency (y-axis). Draw a horizontal line from 25 to the ogive curve. From the point where it intersects the curve, drop a vertical line to the x-axis (Size). The point where this line intersects the x-axis is the median value. Based on the description it equals approximately 26.

5. Calculate cumulative frequencies for "less than" ogive for question 3

To construct the "less than" ogive, calculate the cumulative frequencies: Marks: 0-5, 5-10, 10-15, 15-20, 20-25, 25-30, 30-35, 35-40 Frequency: 7, 10, 20, 13, 17, 10, 14, 9 Cumulative Frequency (less than): 7, 17, 37, 50, 67, 77, 91, 100

6. Plot the "less than" ogive for question 3

Plot the upper class limits against the cumulative frequencies: Points to plot: (5, 7), (10, 17), (15, 37), (20, 50), (25, 67), (30, 77), (35, 91), (40, 100) Draw a smooth curve through these points.

7. Calculate cumulative frequencies for "more than" ogive for question 3

To construct the "more than" ogive, calculate the cumulative frequencies from the highest class interval: Marks: 0-5, 5-10, 10-15, 15-20, 20-25, 25-30, 30-35, 35-40 Frequency: 7, 10, 20, 13, 17, 10, 14, 9 Cumulative Frequency (more than): 100, 93, 83, 63, 50, 33, 23, 9

8. Plot the "more than" ogive for question 3

Plot the lower class limits against the cumulative frequencies: Points to plot: (0, 100), (5, 93), (10, 83), (15, 63), (20, 50), (25, 33), (30, 23), (35, 9) Draw a smooth curve through these points.

9. Determine the median from the intersection for question 3

The median is the x-coordinate of the point where the "less than" and "more than" ogives intersect. This approximately equals 20.