Analyze the relationships based on the given sets of inequalities and equalities.
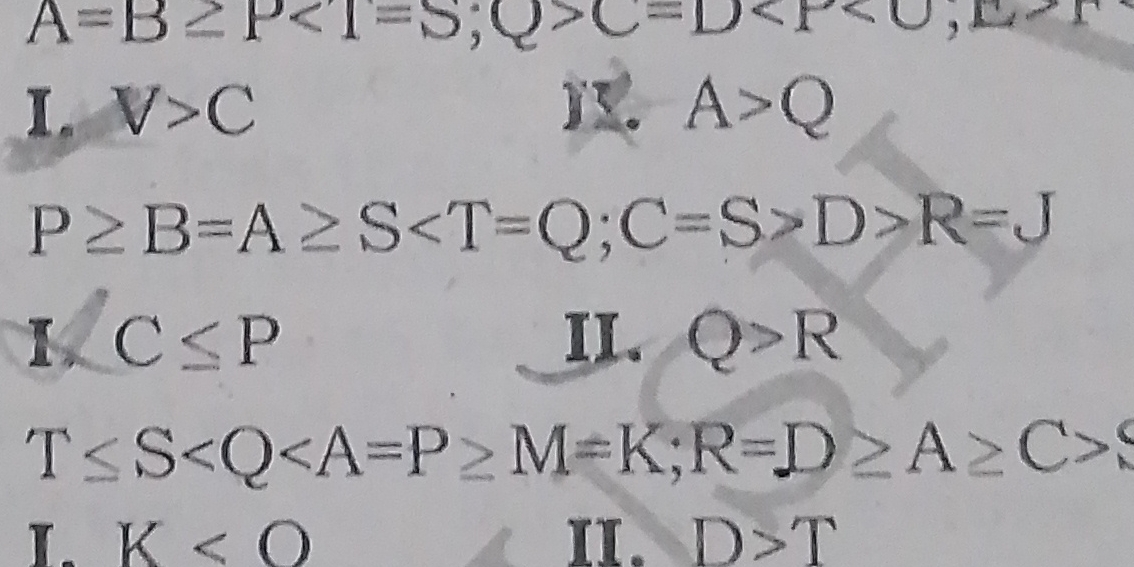
Understand the Problem
The question appears to involve the relation of various entities based on a set of inequalities or equalities. It asks to analyze these relationships to determine a specific order among the entities listed.
Answer
Both statements are false: I. $V < C$ is false; II. $Q < R$ is false.
Answer for screen readers
The correct answer is both statements are False.
Steps to Solve
-
Understanding Inequalities
The problem involves multiple inequalities among various entities. We need to interpret these inequalities to find the relationships among the elements.
-
Breaking Down the Given Relations
The first line states: $$ A = B \geq P \leq T = S; Q < C = D < P < U; E > F $$ From this, we can list the relationships:
- $A = B \geq P$
- $P \leq T = S$
- $Q < C = D$
- $D < P < U$
- $E > F$
-
Organizing the Relationships
The second line states: $$ P \geq B = A \geq S < T \leq Q; C \leq S > D > R = J $$ This shows:
- $P \geq B = A \geq S < T \leq Q$
- $C \leq S > D$
- $D > R = J$
-
Evaluating Further Conditions
The third line provides: $$ T \leq S < Q < A = P \geq M = K; R = D \geq A > C \leq S $$ Which leads to these relationships:
- $T \leq S < Q < A = P \geq M = K$
- $R = D \geq A > C \leq S$
-
Comparing and Validating Statements I and II
We have two statements to evaluate:
- I. $V < C$
- II. $Q < R$ From the inequalities established, we can check the validity of these statements by comparing them with our earlier findings.
-
Construct a Final Order
We must find a final comparative order of all the elements and evaluate the statements to decide their validity in relation to this order.
The correct answer is both statements are False.
More Information
This means based on the established relationships among the entities, I. $V < C$ does not hold true, as C is larger than other entities. Likewise, II. $Q < R$ is also false since R cannot be determined to be less than Q based on the established relationships.
Tips
- Misreading Inequalities: It's easy to overlook the direction of inequalities. Always double-check each relationship.
- Assuming Equalities Imply Larger Values: Just because two entities are equal does not mean they are greater or lesser than all others; be cautious about comparisons.
- Neglecting Transitive Relationships: Remember to apply transitive properties of inequalities consistently.
AI-generated content may contain errors. Please verify critical information