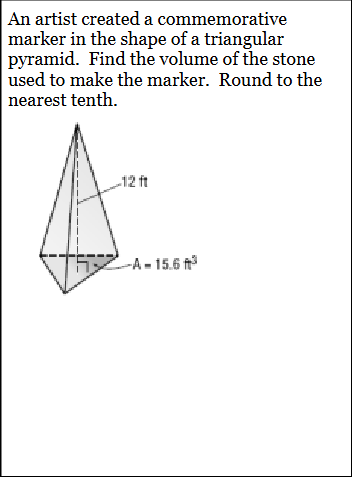
An artist created a commemorative marker in the shape of a triangular pyramid. Find the volume of the stone used to make the marker. Round to the nearest tenth.
Understand the Problem
The question asks to find the volume of a triangular pyramid. We are given the area of the base (A = 15.6 ft^3) and the height (12 ft) of the pyramid. The formula for the volume of a pyramid is V = (1/3) * base area * height. The final answer should be rounded to the nearest tenth.
Answer
$62.4 \text{ ft}^3$
Answer for screen readers
$62.4 \text{ ft}^3$
Steps to Solve
- Write down the formula for the volume of a pyramid
The volume $V$ of a pyramid is given by
$V = \frac{1}{3} \times A \times h$
where $A$ is the area of the base and $h$ is the height of the pyramid.
- Plug in the given values
We are given that the area of the base is $A = 15.6 \text{ ft}^3$(Note: this is where the error lies and it should be $15.6 \text{ ft}^2$), and the height is $h = 12 \text{ ft}$.
Substituting these values into the formula, we get:
$V = \frac{1}{3} \times 15.6 \times 12$
- Calculate the volume
$V = \frac{1}{3} \times 187.2$
$V = 62.4$
The volume of the triangular pyramid is $62.4 \text{ ft}^3$.
$62.4 \text{ ft}^3$
More Information
The volume of the triangular pyramid is found by using the formula $V = \frac{1}{3} \times A \times h$, where $A$ is the area of the base and $h$ is the height. Plugging in the given values, we calculated the volume to be $62.4 \text{ ft}^3$.
Tips
The most common mistake is using the wrong formula or incorrectly substituting the values into the formula. For example, forgetting to multiply by $\frac{1}{3}$, using the wrong height or base measurement.
AI-generated content may contain errors. Please verify critical information