Add -1/2 + 3/5. Write your answer in simplest form.

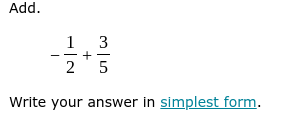
Understand the Problem

The question is asking us to add the fractions -1/2 and 3/5, and then express the answer in its simplest form.

Answer

The answer is $\frac{1}{10}$.

Steps to Solve

Find a common denominator

To add the fractions $-\frac{1}{2}$ and $\frac{3}{5}$, we first need a common denominator. The denominators are 2 and 5. The least common multiple of 2 and 5 is 10.

Convert the fractions

Now we convert both fractions to have the common denominator of 10:

[ -\frac{1}{2} = -\frac{1 \times 5}{2 \times 5} = -\frac{5}{10} ]

[ \frac{3}{5} = \frac{3 \times 2}{5 \times 2} = \frac{6}{10} ]

Add the fractions

Now that both fractions have the same denominator, we can add them:

[ -\frac{5}{10} + \frac{6}{10} = \frac{-5 + 6}{10} = \frac{1}{10} ]

Express in simplest form

The result $\frac{1}{10}$ is already in its simplest form.

The sum of $-\frac{1}{2} + \frac{3}{5}$ in simplest form is $\frac{1}{10}$.

More Information

Adding fractions involves finding a common denominator, which allows us to combine the numerators directly. The final result, $\frac{1}{10}$, indicates that the total is a small positive fraction that can be easily interpreted in various mathematical contexts.

Tips

Not finding the least common denominator: It's essential to find the smallest common multiple of the denominators before adding.
Failing to convert both fractions: Both fractions must be expressed with the common denominator.
Not simplifying the final result: Always check if the fraction can be simplified, though in this case, $\frac{1}{10}$ is already in simplest form.

Thank you for voting!