A wave has the equation (x in meters and t in seconds) y = 0.02 sin (30 t - 4 x). Find: a. Its frequency, speed, and wave length. b. The equation of wave with double amplitude bu... A wave has the equation (x in meters and t in seconds) y = 0.02 sin (30 t - 4 x). Find: a. Its frequency, speed, and wave length. b. The equation of wave with double amplitude but traveling in the opposite direction.
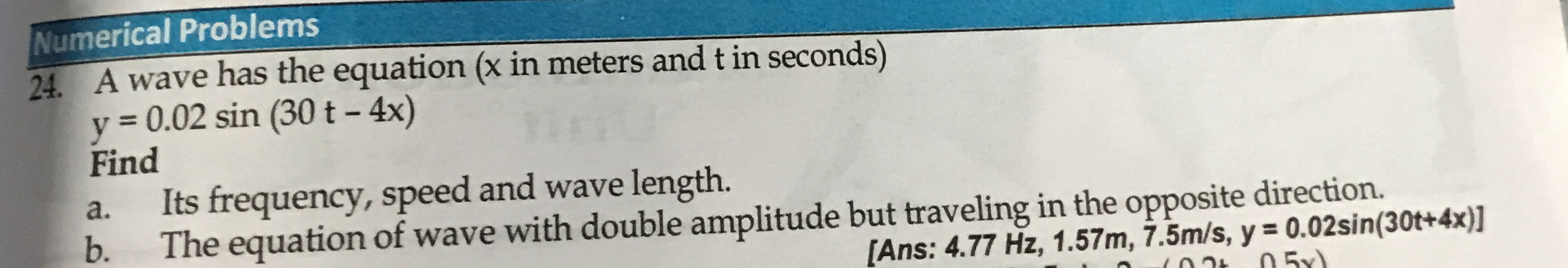
Understand the Problem
The question is asking for two parts: (a) to find the frequency, speed, and wavelength of a given wave, and (b) to derive the equation of the same wave with double the amplitude but moving in the opposite direction.
Answer
Frequency: $4.77 \text{ Hz}$, Speed: $7.48 \text{ m/s}$, Wavelength: $1.57 \text{ m}$, New equation: $y = 0.04 \sin(30t + 4x)$
Answer for screen readers
- Frequency: ( 4.77 \text{ Hz} )
- Speed: ( 7.48 \text{ m/s} )
- Wavelength: ( 1.57 \text{ m} )
- New wave equation: ( y = 0.04 \sin(30t + 4x) )
Steps to Solve
- Identify wave equation parameters
The given wave equation is ( y = 0.02 \sin(30t - 4x) ).
From this, we identify:
- The angular frequency ( \omega = 30 ) (coefficient of ( t ))
- The wave number ( k = 4 ) (coefficient of ( x ))
- Calculate frequency ( f )
Frequency can be calculated using the formula:
$$ f = \frac{\omega}{2\pi} $$
Substituting in the value of ( \omega ):
$$ f = \frac{30}{2\pi} \approx 4.77 \text{ Hz} $$
- Calculate wave speed ( v )
Wave speed can be obtained from the relationship:
$$ v = f \cdot \lambda $$
Where ( \lambda ) (wavelength) can be determined by:
$$ \lambda = \frac{2\pi}{k} $$
Calculate ( \lambda ):
$$ \lambda = \frac{2\pi}{4} \approx 1.57 \text{ m} $$
Now substitute ( \lambda ) into the wave speed formula:
$$ v = f \cdot \lambda = 4.77 \text{ Hz} \cdot 1.57 \text{ m} \approx 7.48 \text{ m/s} $$
- Determine wave equation with double amplitude
The amplitude of the wave is doubled. The original amplitude is ( 0.02 ), so the new amplitude is ( 0.04 ).
The wave traveling in the opposite direction has the form ( y = A \sin(\omega t + kx) ).
Thus, the new equation becomes:
$$ y = 0.04 \sin(30t + 4x) $$
- Frequency: ( 4.77 \text{ Hz} )
- Speed: ( 7.48 \text{ m/s} )
- Wavelength: ( 1.57 \text{ m} )
- New wave equation: ( y = 0.04 \sin(30t + 4x) )
More Information
This problem illustrates the relationship between wave properties: frequency, speed, and wavelength are interconnected through formulas derived from wave mechanics. Doubling the amplitude changes only the height of the wave, while reversing the direction involves changing the sign of the wave number.
Tips
- Confusing the sign in the wave equation. Make sure to correctly identify the wave's direction.
- Miscalculating ( \lambda ) using incorrect formulas. Always use the wavelength calculation ( \lambda = \frac{2\pi}{k} ).
AI-generated content may contain errors. Please verify critical information