A rectangle is x inches wide and 3y inches long. If the length plus twice the width is 12 inches and the length plus the width is 9 inches, what is the length?
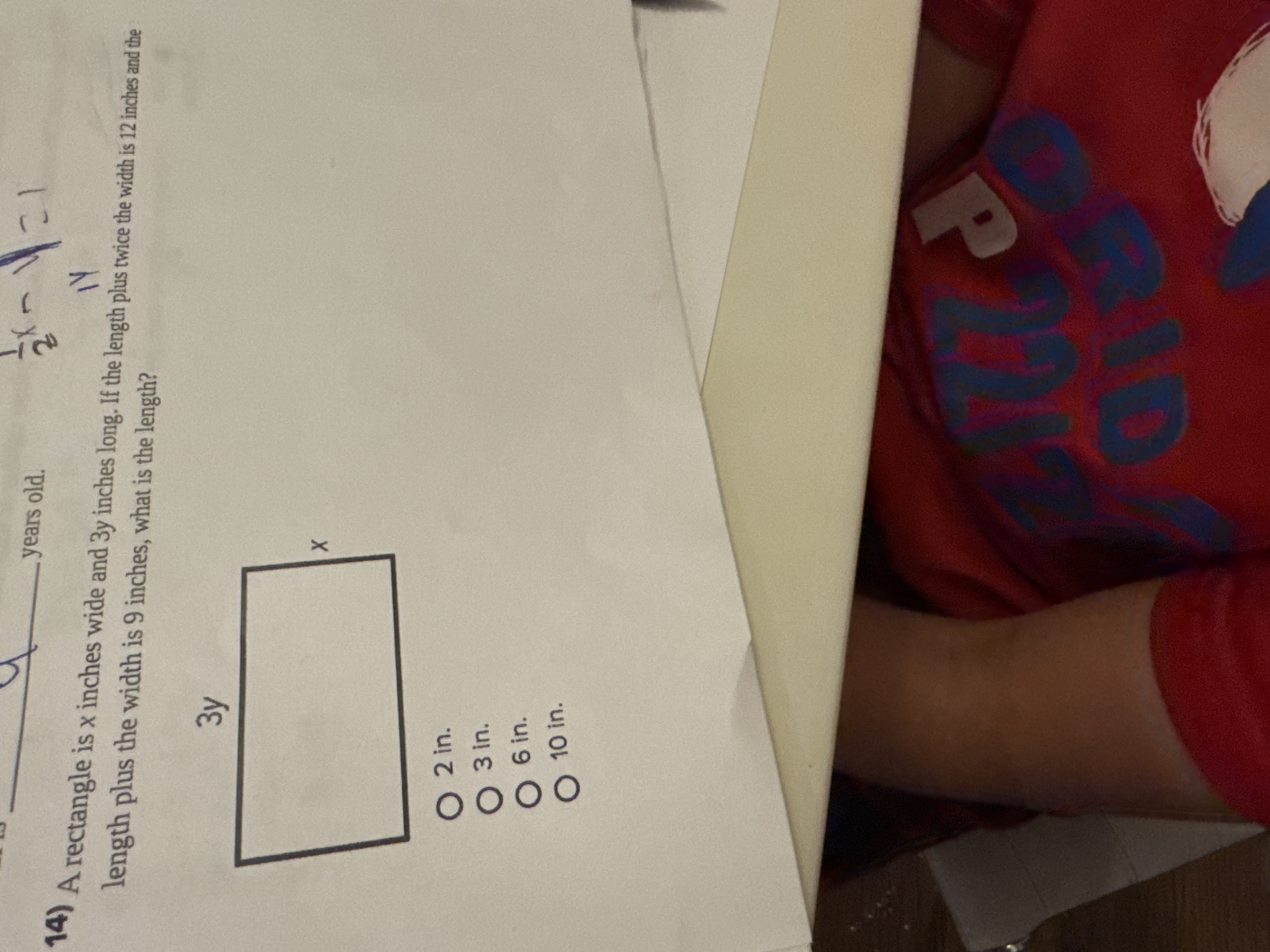
Understand the Problem
The question describes a rectangle with width 'x' and length '3y'. It gives two equations: length plus twice the width equals 12 inches, and length plus the width equals 9 inches. The goal is to find the value of x.
Answer
6 in.
Answer for screen readers
The length of the rectangle is 6 inches.
Steps to Solve
-
Write down the given equations We are given that the length of the rectangle is $3y$ and the width is $x$. The two equations can be written as: $$ 3y + 2x = 12 $$ $$ 3y + x = 9 $$
-
Solve for x Subtract the second equation from the first to eliminate $3y$: $$ (3y + 2x) - (3y + x) = 12 - 9 $$ $$ 3y + 2x - 3y - x = 3 $$ $$ x = 3 $$
-
Find the length $3y$ Substitute $x = 3$ into the second equation: $$ 3y + x = 9 $$ $$ 3y + 3 = 9 $$ $$ 3y = 9 - 3 $$ $$ 3y = 6 $$
The length of the rectangle is 6 inches.
More Information
The length is $3y = 6$ inches and the width is $x = 3$ inches.
Tips
A common mistake is to solve for x instead of $3y$. Make sure to read the question carefully.
AI-generated content may contain errors. Please verify critical information