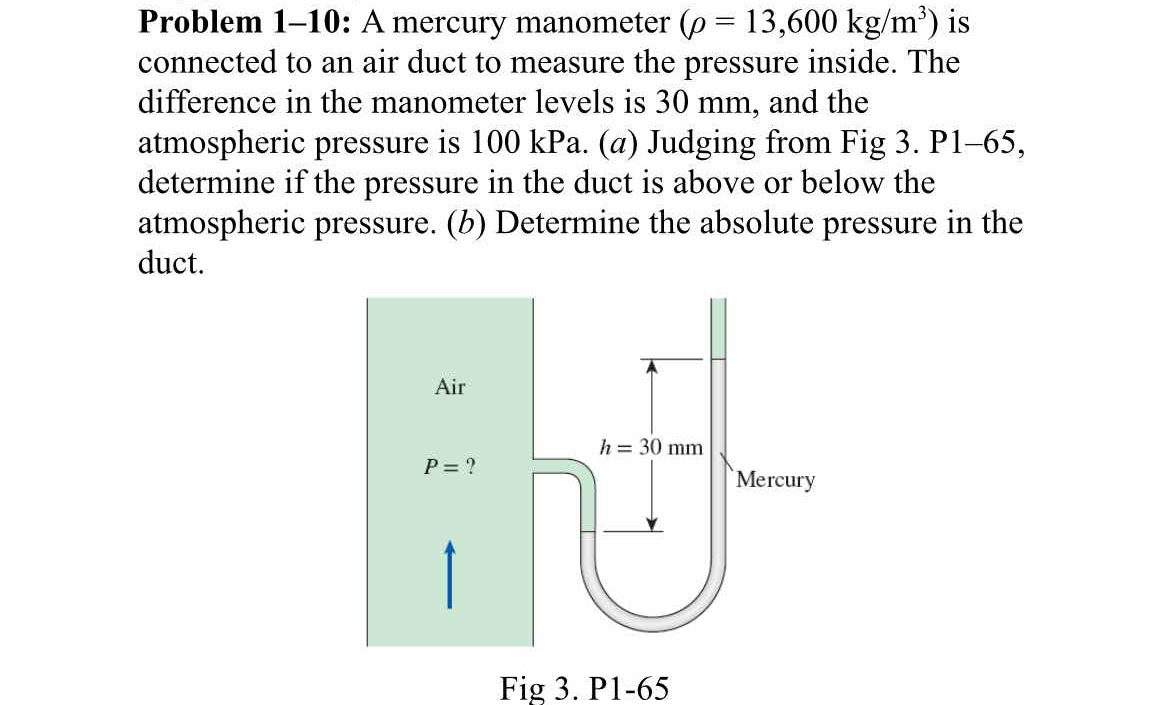
A mercury manometer with a density of 13,600 kg/m³ is connected to an air duct measuring pressure inside. The manometer levels show a difference of 30 mm and atmospheric pressure i... A mercury manometer with a density of 13,600 kg/m³ is connected to an air duct measuring pressure inside. The manometer levels show a difference of 30 mm and atmospheric pressure is 100 kPa. (a) Determine if the pressure in the duct is above or below atmospheric pressure. (b) Determine the absolute pressure in the duct. Read more

Steps to Solve

1. Identify the parameters We have the following information:

• Density of mercury, $\rho = 13,600 , \text{kg/m}^3$
• Height difference in the manometer, $h = 30 , \text{mm} = 0.03 , \text{m}$
• Atmospheric pressure, $P_{atm} = 100 , \text{kPa} = 100,000 , \text{Pa}$

2. Calculate the pressure difference using hydrostatic pressure equation The pressure difference due to the height of the mercury column can be calculated using the hydrostatic pressure equation: $$ \Delta P = \rho g h $$ Where $g \approx 9.81 , \text{m/s}^2$ (acceleration due to gravity).

Calculating $\Delta P$: $$ \Delta P = 13,600 , \text{kg/m}^3 \times 9.81 , \text{m/s}^2 \times 0.03 , \text{m} $$

3. Determine the calculated pressure difference Plugging in the values: $$ \Delta P = 13,600 \times 9.81 \times 0.03 $$ Calculating gives: $$ \Delta P = 4,000.88 , \text{Pa} $$

4. Determine the pressure in the duct Since the mercury level is lower on the duct side than the atmospheric side, the pressure in the duct is: $$ P = P_{atm} - \Delta P $$ Thus, substituting: $$ P = 100,000 , \text{Pa} - 4,000.88 , \text{Pa} $$

5. Calculate absolute pressure Now, we calculate the absolute pressure in the duct: $$ P = 100,000 - 4,000.88 = 96,000.12 , \text{Pa} $$