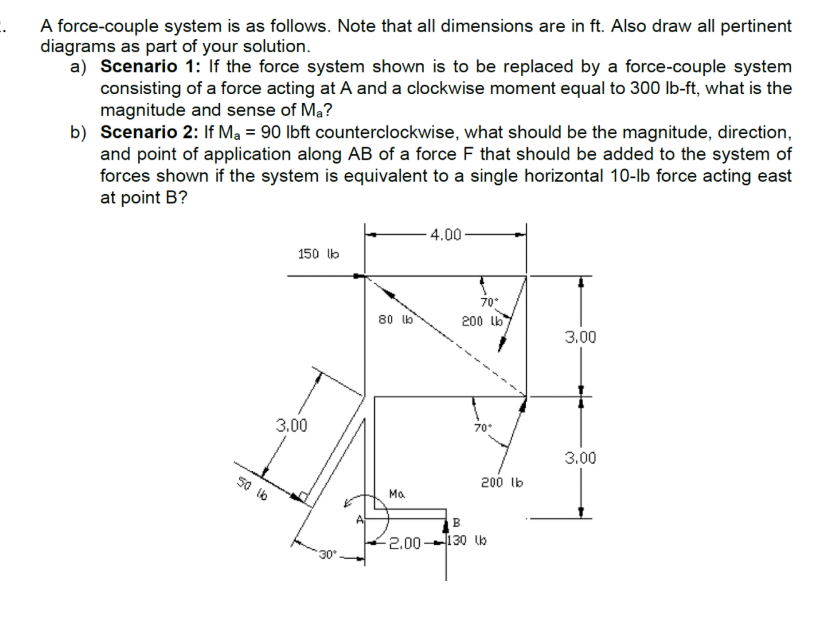
A force-couple system is as follows. Note that all dimensions are in ft. Also draw all pertinent diagrams as part of your solution. a) Scenario 1: If the force system shown is to... A force-couple system is as follows. Note that all dimensions are in ft. Also draw all pertinent diagrams as part of your solution. a) Scenario 1: If the force system shown is to be replaced by a force-couple system consisting of a force acting at A and a clockwise moment equal to 300 lb-ft, what is the magnitude and sense of $M_a$? b) Scenario 2: If $M_a$ = 90 lbft counterclockwise, what should be the magnitude, direction, and point of application along AB of a force F that should be added to the system of forces shown if the system is equivalent to a single horizontal 10-lb force acting east at point B? Read more

Steps to Solve

1. Calculate the moment due to the 150 lb force about point A

The perpendicular distance from the line of action of the 150 lb force to point A is 3 ft. The moment created by the 150 lb force about point A is:

$M_{150} = 150 \cdot 3 = 450 \text{ lb-ft (clockwise)}$

2. Calculate the moment due to the 50 lb force about point A

The perpendicular distance from the line of action of the 50 lb force to point A is 3 ft. The moment created by the 50 lb force about point A is:

$M_{50} = 50 \cdot 3 = 150 \text{ lb-ft (counterclockwise)}$

3. Calculate the moment due to the 80 lb force about point A

The vertical component of the 80 lb force is $80\sin(30^\circ) = 80 \cdot 0.5 = 40 \text{ lb}$. The horizontal component of the 80 lb force is $80\cos(30^\circ) = 80 \cdot \frac{\sqrt{3}}{2} = 40\sqrt{3} \approx 69.28 \text{ lb}$. The moment created by the 80 lb force about point A is:

$M_{80} = (40 \cdot 4) + (40\sqrt{3} \cdot 3) \approx 160 + 207.84 = 367.84 \text{ lb-ft (clockwise)}$.

4. Calculate the moment due to the 200 lb force (top) about point A

The vertical component of the 200 lb force is $200\sin(70^\circ) \approx 200 \cdot 0.94 = 188 \text{ lb}$. The horizontal component of the 200 lb force is $200\cos(70^\circ) \approx 200 \cdot 0.34 = 68.4\text{ lb} $. The moment created by the 200 lb force (top) about point A is:

$M_{200, top} = (188 \cdot 4) - (68.4 \cdot 3) \approx 752 - 205.2 = 546.8 \text{ lb-ft (clockwise)}$

5. Calculate the moment due to the 200 lb force (bottom) about point A

The vertical component of the 200 lb force is $200\sin(70^\circ) \approx 200 \cdot 0.94 = 188 \text{ lb}$. The horizontal component of the 200 lb force is $200\cos(70^\circ) \approx 200 \cdot 0.34 = 68.4 \text{ lb}$. The moment created by the 200 lb force (bottom) about point A is:

$M_{200, bottom} = (188 \cdot 0) + (68.4 \cdot 3) \approx 0 + 205.2 = 205.2 \text{ lb-ft (counterclockwise)}$

6. Calculate the moment due to the 130 lb force about point A

$M_{130} = 130 \cdot 2 = 260 \text{ lb-ft (counterclockwise)}$

7. Calculate the total moment about point A

$M_A = -450 + 150 - 367.84 - 546.8 + 205.2 + 260 =-774.44 \text{ lb-ft} $ The negative indicates a clockwise moment.

8. Calculate $M_a$

Since the system is to be replaced by a force at A and a clockwise moment of 300 lb-ft, $$M_A = -300$$ $$M_a = M_A + 300 = -749.44 + 300 = - 474.44 \text{ lb-ft} $$ Therefore, magnitude of $M_a$ is $474.44 \text{ lb-ft}$. Since the result is negative, $M_a$ is clockwise.

9. Part b: Calculate the resultant force of the original system.

Horizontal forces: $150 - 80\cos(30^\circ) + 200\cos(70^\circ) + 200\cos(70^\circ) -130 \approx 150 - 69.28 + 68.4 + 68.4 - 130 = 87.52 \text{ lb (east)}$ Vertical forces: $-50 - 80\sin(30^\circ) - 200\sin(70^\circ) - 200\sin(70^\circ) \approx -50 - 40 - 188 - 188 = -466 \text{ lb (down)}$

10. Part b: Calculate the resultant force required to get a 10 lb force at B.

Let $F_x$ and $F_y$ be the horizontal and vertical components of the force $F$ that must be added. The new horizontal force is $87.52 + F_x = 10 \text{ lb}$. Therefore, $F_x = -77.52 \text{ lb}$ (West). The new vertical force is $-466 + F_y = 0$. Therefore, $F_y = 466 \text{ lb}$ (Up).

11. Part b: Calculate the magnitude and direction of F.

$|F| = \sqrt{(-77.52)^2 + (466)^2} \approx \sqrt{6009.35 + 217156} \approx \sqrt{223165.35} \approx 472.4 \text{ lb}$

$\theta = \arctan(\frac{466}{-77.52}) \approx -80.5^\circ$ Since $F_x$ is negative and $F_y$ is positive, this is in the second quadrant. Therefore, $\theta \approx 180^\circ - 80.5^\circ = 99.5^\circ$ (measured counterclockwise from the positive x-axis).

12. Part b: Calculate where the force F must be applied along AB.

The moment about B due to external forces must be zero, since the equivalent force acts at B. The moment about B due to the original forces is $M_A = -90 \text{ lb-ft} + 130 \cdot 2 = 170 \text{ lb-ft (counterclockwise)}$.

The moment about B due to the additional force F must cancel this moment, so the moment about B due to F is $-170 \text{ lb-ft (clockwise)}$. Let $d$ be the distance from A to the location where the force F is applied on line AB. The moment about B due to the force F is $M_F = -F_y \cdot d \cdot \cos(30^\circ) - F_x \cdot d \cdot \sin(30^\circ) = -170$. $$-466 \cdot d \cdot \cos(30^\circ) - (-77.52) \cdot d \cdot \sin(30^\circ) = -170$$ $$-466 \cdot d \cdot \frac{\sqrt{3}}{2} + 77.52 \cdot d \cdot \frac{1}{2} = -170$$ $$-403.57 d + 38.76 d = -170$$ $$-364.81 d = -170$$ $$d = \frac{170}{364.81} \approx 0.466 \text{ ft}$$ Therefore, the force F should be applied a distance of 0.466 ft along AB from A.