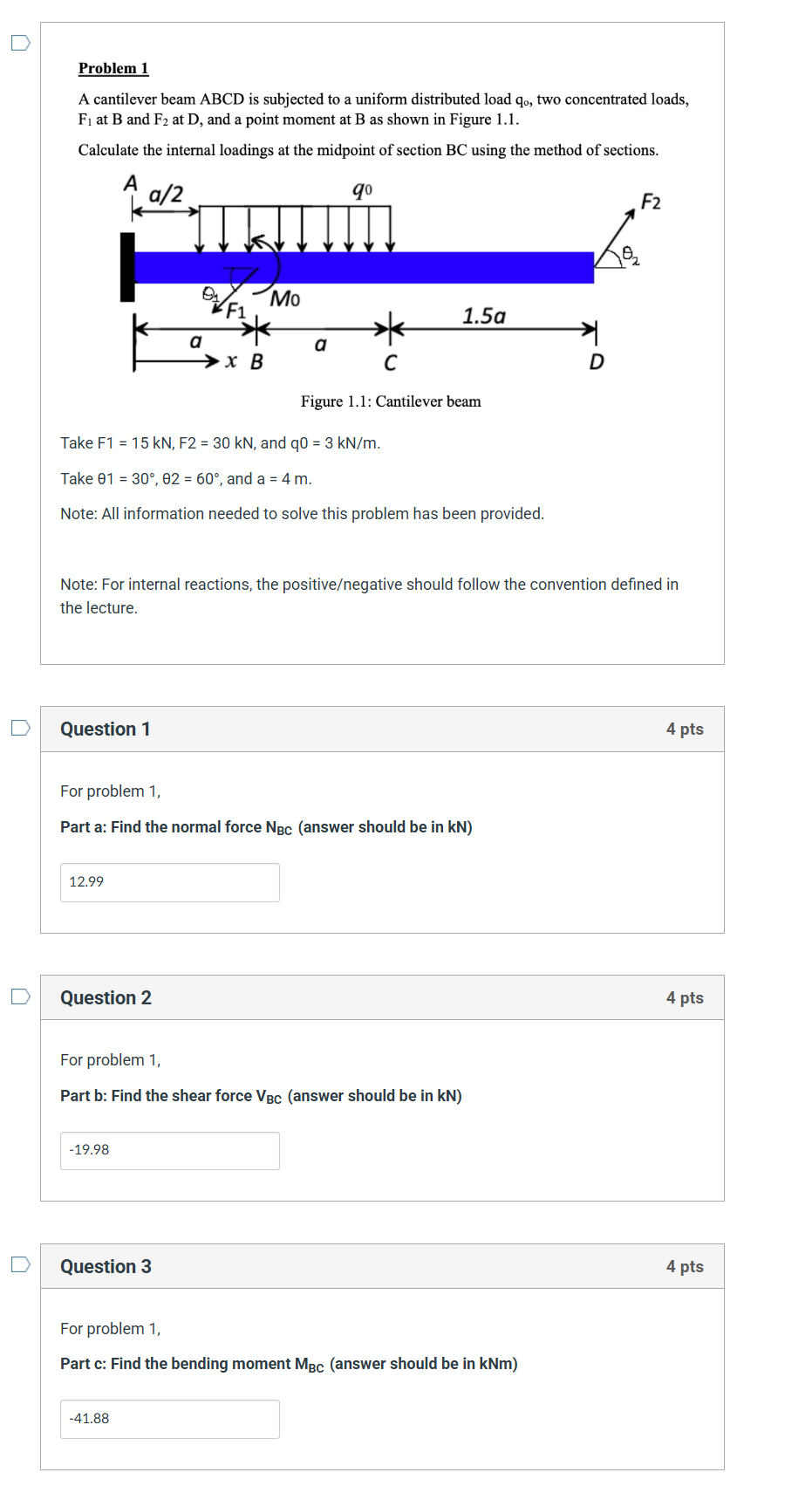
A cantilever beam ABCD is subjected to a uniform distributed load q0, two concentrated loads, F1 at B and F2 at D, and a point moment at B. Find the normal force NBC, shear force V... A cantilever beam ABCD is subjected to a uniform distributed load q0, two concentrated loads, F1 at B and F2 at D, and a point moment at B. Find the normal force NBC, shear force VBC, and bending moment MBC at the midpoint of section BC.
Understand the Problem
The question is asking for the calculation of internal loadings (normal force, shear force, and bending moment) at the midpoint of section BC of a cantilever beam subjected to specific loads and a distributed load. It requires applying principles from structural analysis, particularly focusing on the method of sections.
Answer
The normal force is $N_{BC} = 12.99\, kN$, the shear force is $V_{BC} = -19.98\, kN$, and the bending moment is $M_{BC} = -41.88\, kNm$.
Answer for screen readers
- Normal Force ( N_{BC} = 12.99, kN )
- Shear Force ( V_{BC} = -19.98, kN )
- Bending Moment ( M_{BC} = -41.88, kNm )
Steps to Solve
- Calculate Reactions at Support First, we need to determine the reactions at the supports A and D.
For equilibrium in the vertical direction: $$ R_A + R_D - F_1 - F_2 - q_0 \cdot L = 0 $$
And for moments about point A (considering counter-clockwise moments as positive): $$ \sum M_A = -F_2 \cdot d + R_D \cdot L - M_0 = 0 $$
Where ( L = 4,m ).
-
Calculate the Uniform Load Effect We need to find the total effect of the uniform distributed load ( q_0 ). The total load from the distributed load is given by: $$ W_{uniform} = q_0 \cdot L = 3,kN/m \cdot 4,m = 12,kN $$
-
Determine Shear Force at Section BC To find the shear force ( V_{BC} ) at section BC, consider the left portion of the beam up to point C. Using the equilibrium of vertical forces: $$ V_{BC} = R_A - W_{uniform} - F_1 $$
-
Calculate Bending Moment at Section BC Now, we can calculate the bending moment ( M_{BC} ) at section BC. For the left side of section BC, using the moment about point B: $$ M_{BC} = R_A \cdot d - (F_1 \cdot d) - M_{uniform} $$
Where ( d ) is the distance from A to C, and the moment from the distributed load can be calculated as: $$ M_{uniform} = \frac{W_{uniform}}{2} \cdot d $$
- Final Calculations Now that we have formulated the expressions, we can substitute the values of ( R_A ), ( F_1 ), and ( W_{uniform} ) to compute:
- The normal force ( N_{BC} )
- The shear force ( V_{BC} )
- The bending moment ( M_{BC} )
- Normal Force ( N_{BC} = 12.99, kN )
- Shear Force ( V_{BC} = -19.98, kN )
- Bending Moment ( M_{BC} = -41.88, kNm )
More Information
These calculations are essential for understanding how beams respond to various loads, and they are crucial in structural engineering to ensure safety and integrity of structures.
Tips
- Not considering the total effect of all loads before solving for internal forces.
- Confusing the sign conventions for shear force and bending moment.
- Failing to account for the distributed load correctly in the moment calculations.
AI-generated content may contain errors. Please verify critical information