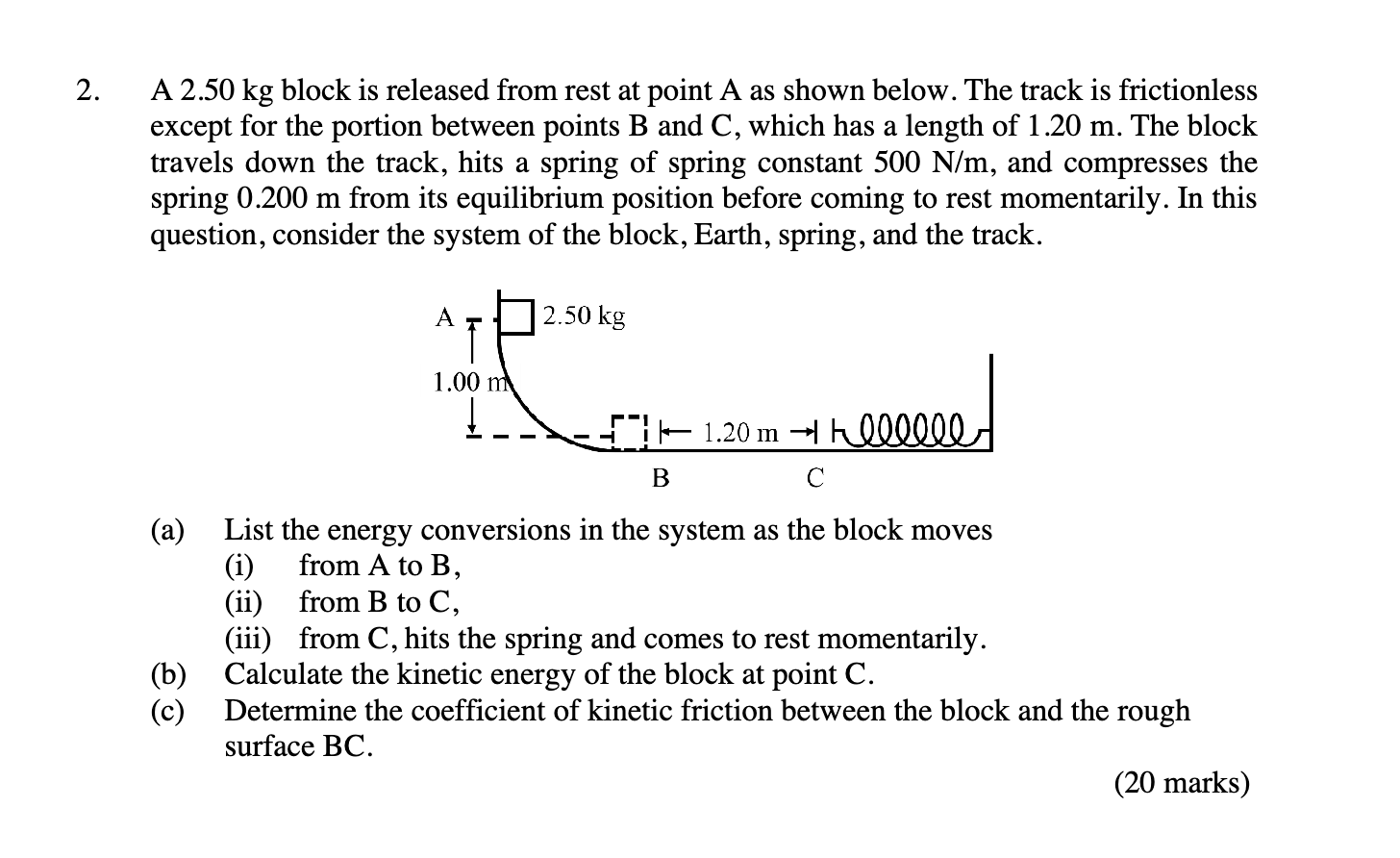
A 2.50 kg block is released from rest at point A as shown below. The track is frictionless except for the portion between points B and C, which has a length of 1.20 m. The block tr... A 2.50 kg block is released from rest at point A as shown below. The track is frictionless except for the portion between points B and C, which has a length of 1.20 m. The block travels down the track, hits a spring of spring constant 500 N/m, and compresses the spring 0.200 m from its equilibrium position before coming to rest momentarily. In this question, consider the system of the block, Earth, spring, and the track. (a) List the energy conversions in the system as the block moves (i) from A to B, (ii) from B to C, (iii) from C, hits the spring and comes to rest momentarily. (b) Calculate the kinetic energy of the block at point C. (c) Determine the coefficient of kinetic friction between the block and the rough surface BC. Read more

Steps to Solve

1. Energy conversions from A to B

From A to B, the block slides down a frictionless track. Gravitational potential energy is converted into kinetic energy.

2. Energy conversions from B to C

From B to C, the track is rough, so kinetic energy is converted into thermal energy due to friction.

3. Energy conversions from C to spring compression

From C to the point where the spring is compressed, kinetic energy is converted into spring potential energy.

4. Kinetic energy at point B

First find the potential energy at point A, using $PE = mgh$ where $m = 2.50 \ kg$, $g = 9.8 \ m/s^2$ and $h = 1.00 \ m$. $$PE = (2.50 \ kg)(9.8 \ m/s^2)(1.00 \ m) = 24.5 \ J$$ Because the track is frictionless between A and B, the potential energy at A converts entirely to kinetic energy at B: $KE_B = 24.5 \ J$

5. Kinetic energy at point C

Use the Work-Energy Theorem to calculate the kinetic energy at point C. The work done by friction is $W_f = -f_k d = -\mu_k mgd$, where $d = 1.20 \ m$. However, we don't know $\mu_k$ yet, so we will rearrange our equation. The work done by friction is equal to the change in kinetic energy between points B and C: $W_f = KE_C - KE_B$. So, $KE_C = KE_B + W_f$. We also know that the energy stored in the spring is equal to the kinetic energy at point C. The potential energy stored in the spring is $PE_{spring} = \frac{1}{2}kx^2$, where $k = 500 \ N/m$ and $x = 0.200 \ m$. $$PE_{spring} = \frac{1}{2}(500 \ N/m)(0.200 \ m)^2 = 10 \ J$$ Therefore the kinetic energy at point C: $KE_C = 10 \ J$

6. Calculate the coefficient of kinetic friction

We know that the work done by friction between B and C is the change in kinetic energy between B and C: $W_f = KE_C - KE_B = 10 \ J - 24.5 \ J = -14.5 \ J$ We also know that the work done by friction can be defined as $W_f = -f_k d = -\mu_k mg d$. By equating these two formulas, we can solve for $\mu_k$. $$-14.5 \ J = -\mu_k (2.50 \ kg)(9.8 \ m/s^2)(1.20 \ m)$$ $$\mu_k = \frac{14.5 \ J}{(2.50 \ kg)(9.8 \ m/s^2)(1.20 \ m)} = 0.492$$