(3/4)^3
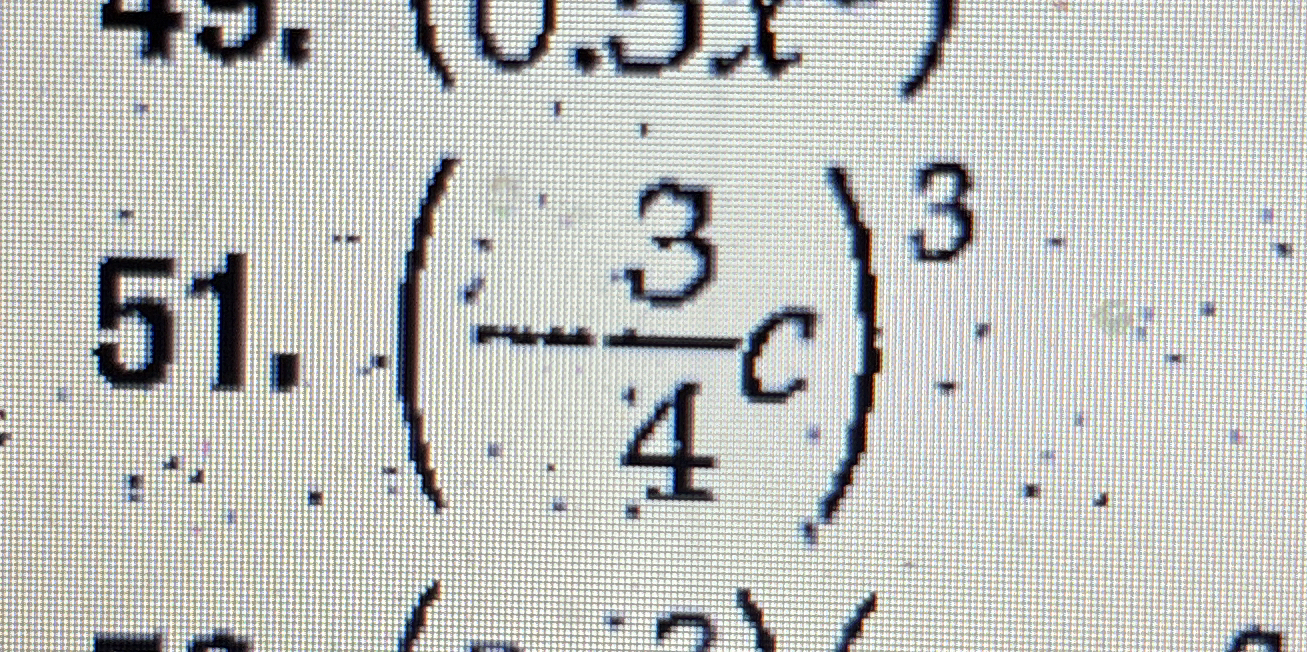
Understand the Problem
The question appears to be about simplifying or evaluating an expression that involves a fraction raised to a power, specifically (3/4)^3.
Answer
The simplified expression is \(\frac{27}{64}\).
Answer for screen readers
The simplified value of (\left( \frac{3}{4} \right)^3) is (\frac{27}{64}).
Steps to Solve
-
Identify the expression
The expression to evaluate is (\left( \frac{3}{4} \right)^3). -
Apply the exponent to the fraction
When raising a fraction to a power, raise both the numerator and denominator to that power: $$ \left( \frac{3}{4} \right)^3 = \frac{3^3}{4^3} $$ -
Calculate the numerator and denominator
Now we calculate the numerator and the denominator:- For the numerator: (3^3 = 27)
- For the denominator: (4^3 = 64)
-
Combine the results
Now we can write the fraction with the calculated values: $$ \left( \frac{3}{4} \right)^3 = \frac{27}{64} $$
The simplified value of (\left( \frac{3}{4} \right)^3) is (\frac{27}{64}).
More Information
The expression (\left( \frac{3}{4} \right)^3) is an example of exponentiation applied to fractions. Understanding how to handle fractions when raised to powers is an important skill in mathematics, especially in algebra.
Tips
- Forgetting to apply the exponent to both numerator and denominator: It's essential to remember that when raising a fraction to a power, you must raise both parts to that power.
- Miscalculating the powers: Double-check the calculations of values such as (3^3) and (4^3) to avoid mistakes.
AI-generated content may contain errors. Please verify critical information