(2a^3)(2h^4)^3[(-2g^4h)^3]^2
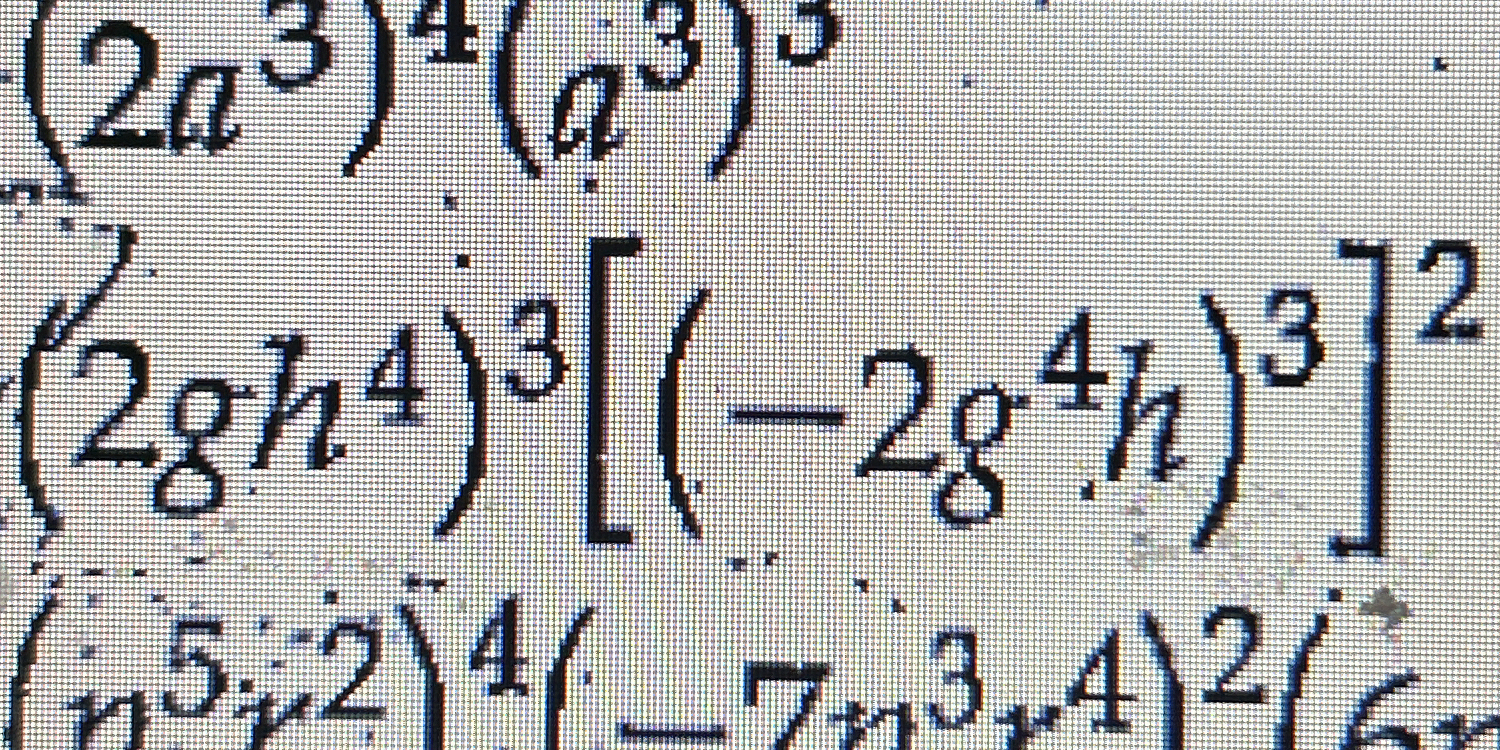
Understand the Problem
The question presents a mathematical expression involving variables and exponents. It likely requires simplification or solving of the expression according to algebraic rules.
Answer
$$1024 a^3 g^{24} h^{18}$$
Answer for screen readers
The final answer is:
$$1024 a^3 g^{24} h^{18}$$
Steps to Solve
-
Expand the Expression
First, we will expand each part of the expression:
$$(2a^3) \cdot (2h^4)^3 \cdot [(-2g^4h)^3]^2$$ -
Calculate Each Term
For $(2h^4)^3$, we apply the power rule:
$$(2h^4)^3 = 2^3 \cdot (h^4)^3 = 8h^{12}$$
For $(-2g^4h)^3$, we apply the same rules:
$$(-2g^4h)^3 = (-2)^3 \cdot (g^4)^3 \cdot h^3 = -8g^{12}h^3$$ -
Square the Result
Now we need to square the result from the last term:
$$[(-2g^4h)^3]^2 = (-8g^{12}h^3)^2 = 64g^{24}h^6$$ -
Combine All Terms
Now substitute the expanded results into the expression:
$$(2a^3) \cdot (8h^{12}) \cdot (64g^{24}h^6)$$ -
Calculate the Coefficients
Combine the numbers (coefficients) together:
$$2 \cdot 8 \cdot 64 = 1024$$ -
Combine the Variables
Now combine the variable parts:
- For $h$: $h^{12} \cdot h^6 = h^{12+6} = h^{18}$
- The rest stays the same.
The combined final result is: $$1024 a^3 g^{24} h^{18}$$
The final answer is:
$$1024 a^3 g^{24} h^{18}$$
More Information
This expression showcases the application of the properties of exponents, particularly the power of a product and the power of a power rules.
Tips
- Neglecting to multiply coefficients when expanding expressions.
- Forgetting to add exponents of the same base correctly.
- Misapplying the exponent rules, especially when dealing with negative bases.
AI-generated content may contain errors. Please verify critical information