(√2)³(√5)²
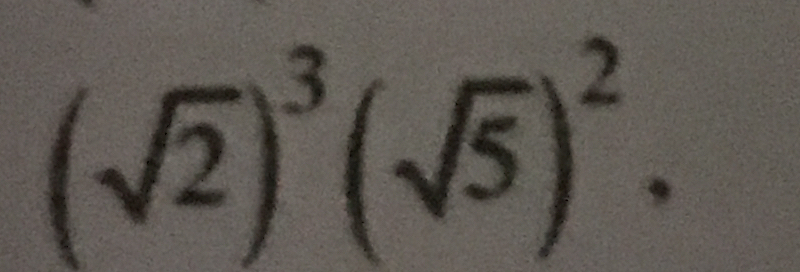
Understand the Problem
The question involves calculating the expression consisting of the square root of 2 raised to the power of 3, multiplied by the square root of 5 raised to the power of 2. The objective is to simplify and find the final value of this expression.
Answer
The final value of the expression is $10\sqrt{2}$.
Answer for screen readers
The final value of the expression is $10\sqrt{2}$.
Steps to Solve
- Calculate the first term $(\sqrt{2})^3$
To simplify $(\sqrt{2})^3$, we can rewrite this as: $$ (\sqrt{2})^3 = (\sqrt{2} \cdot \sqrt{2} \cdot \sqrt{2}) = 2 \cdot \sqrt{2} = 2^{3/2} $$
- Calculate the second term $(\sqrt{5})^2$
Now simplifying $(\sqrt{5})^2$ gives us: $$ (\sqrt{5})^2 = 5 $$
- Combine both results
We now combine the results: $$ 2^{3/2} \cdot 5 $$
- Express $2^{3/2}$ in a simpler form
We can rewrite $2^{3/2}$ as: $$ 2^{3/2} = \sqrt{2^3} = \sqrt{8} $$
Thus: $$ \sqrt{8} \cdot 5 = 5\sqrt{8} $$
- Simplifying further
To simplify $5\sqrt{8}$, we note: $$ \sqrt{8} = \sqrt{4 \cdot 2} = 2\sqrt{2} $$
Finally, we have: $$ 5\sqrt{8} = 5 \cdot 2\sqrt{2} = 10\sqrt{2} $$
The final value of the expression is $10\sqrt{2}$.
More Information
This expression involves properties of exponents and square roots. Understanding how to manipulate these can simplify many mathematical expressions. The calculation shows the relationship between exponents and roots succinctly.
Tips
- Forgetting to apply the exponent to both the base and the square root. Always remember that $(\sqrt{a})^n = a^{n/2}$.
- Miscalculating square roots or not simplifying fully. It's essential to simplify to the lowest radical form if possible.
AI-generated content may contain errors. Please verify critical information