√(16x) * √(16x^5)
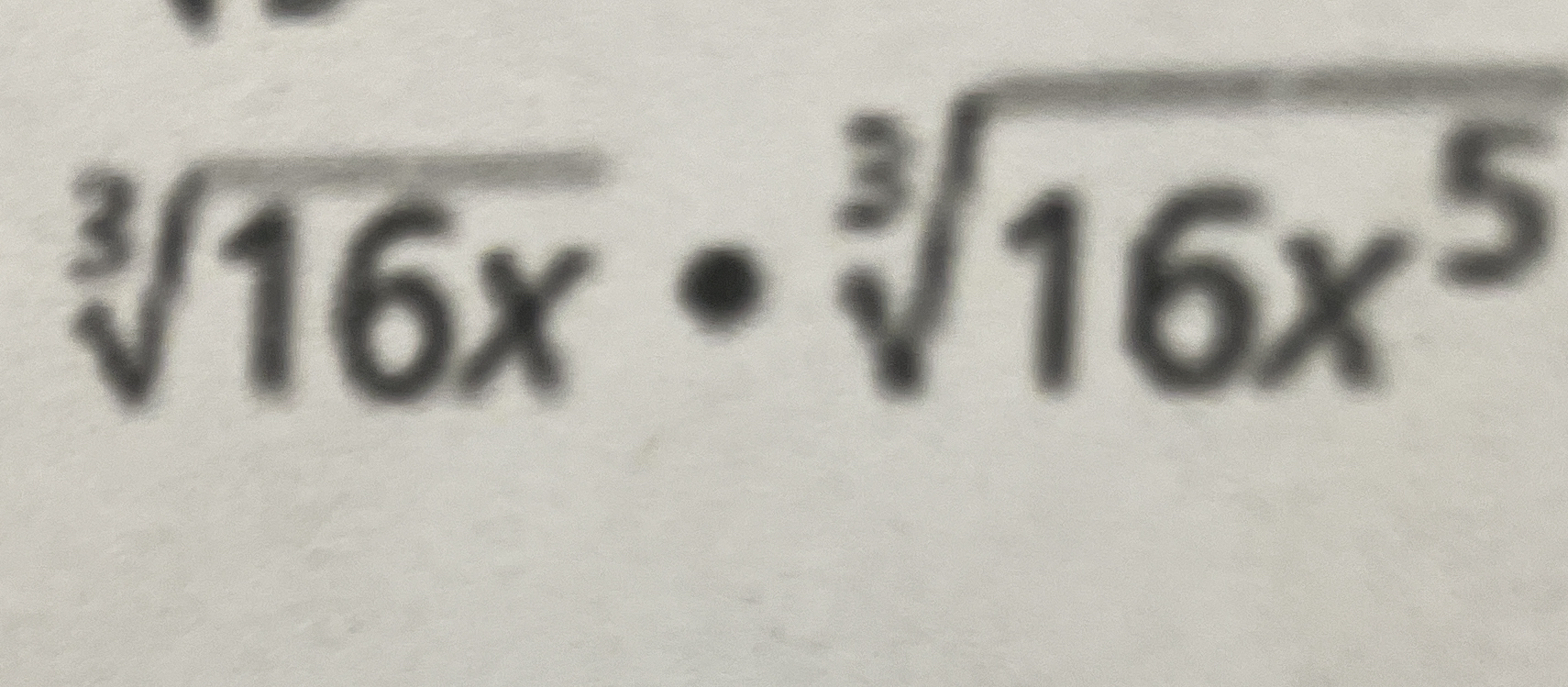
Understand the Problem
The question presents an expression involving cube roots of 16x multiplied by the square root of 16x to the power of 5. It requires simplifying this expression or providing a solution for it.
Answer
The simplified expression is $$ 16^{\frac{5}{6}} \cdot x^{\frac{17}{6}} $$
Answer for screen readers
The simplified expression is
$$ 16^{\frac{5}{6}} \cdot x^{\frac{17}{6}} $$
Steps to Solve
- Rewrite the expressions with exponent notation
The cube root can be expressed as an exponent of $\frac{1}{3}$, and the square root can be expressed as an exponent of $\frac{1}{2}$. Thus, we rewrite the expression:
$$ \sqrt[3]{16x} = (16x)^{\frac{1}{3}} $$
and
$$ \sqrt{16x^5} = (16x^5)^{\frac{1}{2}} $$
- Apply the exponent rules
Next, we can multiply the two expressions together. This involves adding the exponents of common bases:
$$ (16x)^{\frac{1}{3}} \cdot (16x^5)^{\frac{1}{2}} = (16^{\frac{1}{3}} \cdot x^{\frac{1}{3}}) \cdot (16^{\frac{1}{2}} \cdot x^{\frac{5}{2}}) $$
- Combine the bases
Now, we combine the bases of the same type:
$$ 16^{\frac{1}{3} + \frac{1}{2}} \cdot x^{\frac{1}{3} + \frac{5}{2}} $$
- Calculate the new exponents
Calculating $\frac{1}{3} + \frac{1}{2}$ requires a common denominator (which is 6):
$$ \frac{1}{3} = \frac{2}{6} \quad \text{and} \quad \frac{1}{2} = \frac{3}{6} $$
Thus,
$$ \frac{1}{3} + \frac{1}{2} = \frac{2}{6} + \frac{3}{6} = \frac{5}{6} $$
For $x$,
$$ \frac{1}{3} + \frac{5}{2} $$
Again, using a common denominator (which is 6):
$$ \frac{1}{3} = \frac{2}{6} \quad \text{and} \quad \frac{5}{2} = \frac{15}{6} $$
Hence,
$$ \frac{1}{3} + \frac{5}{2} = \frac{2}{6} + \frac{15}{6} = \frac{17}{6} $$
- Final expression
Now we can write the final expression:
$$ 16^{\frac{5}{6}} \cdot x^{\frac{17}{6}} $$
The simplified expression is
$$ 16^{\frac{5}{6}} \cdot x^{\frac{17}{6}} $$
More Information
The expression involves both cube roots and square roots, which were converted to exponent form for easier manipulation. The calculations utilized exponent addition rules and common denominators to simplify the solution effectively.
Tips
- Failing to convert roots into their fractional exponent forms.
- Not using a common denominator when adding fractions, leading to incorrect exponent results.
AI-generated content may contain errors. Please verify critical information