∫ 12cos(4x)dx
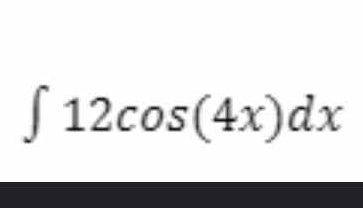
Understand the Problem
The question is asking for the integral of the function 12cos(4x) with respect to x. To solve it, we will apply the basic rules of integration, specifically for cosine functions.
Answer
$$3\sin(4x) + C$$
Answer for screen readers
The integral of the function is: $$3\sin(4x) + C$$
Steps to Solve
-
Identify the integral We need to integrate the function $12\cos(4x)$ with respect to $x$.
-
Use the integration formula for cosine The integral of $\cos(kx)$ is given by: $$\int \cos(kx) , dx = \frac{1}{k} \sin(kx) + C$$ where $C$ is the constant of integration.
-
Apply the formula to the given function In our case, $k = 4$, so we have: $$\int 12\cos(4x) , dx = 12 \cdot \frac{1}{4} \sin(4x) + C$$
-
Simplify the expression Now, simplify to get the final integrated form: $$\int 12\cos(4x) , dx = 3\sin(4x) + C$$
The integral of the function is: $$3\sin(4x) + C$$
More Information
The integral of a cosine function results in a sine function, scaled by the reciprocal of the coefficient in front of $x$. In this case, the factor of 12 is factored out, and the $\frac{1}{4}$ results from integrating the cosine function.
Tips
- Forgetting to include the constant of integration $C$. Always remember that indefinite integrals include a constant since they represent a family of functions.
- Incorrectly applying the formula for integrating cosine functions. Ensure you correctly identify the coefficient in front of $x$ in $\cos(kx)$.
